| NCERT Exemplar Solutions | ||||||
|---|---|---|---|---|---|---|
| 6th | 7th | 8th | 9th | 10th | 11th | 12th |
Chapter 6 Triangles
Welcome to this essential resource providing comprehensive solutions for the Class 10 NCERT Exemplar problems dedicated to the fundamental geometric chapter on Triangles. These Exemplar questions are meticulously designed to move significantly beyond standard textbook exercises, demanding a deeper conceptual understanding and the ability to construct rigorous proofs and solve complex problems involving triangle properties. The primary focus lies on two critical areas: the detailed exploration of triangle similarity and the powerful applications of the Pythagoras theorem. Mastering the challenges presented in the Exemplar is crucial for developing advanced geometric reasoning and problem-solving skills.
A substantial portion of these solutions delves into the concept of similarity of triangles. We explore the necessary and sufficient criteria for establishing similarity:
- AA (Angle-Angle) Similarity: If two angles of one triangle are respectively equal to two angles of another triangle, the triangles are similar.
- SAS (Side-Angle-Side) Similarity: If one angle of a triangle is equal to one angle of another triangle and the sides including these angles are in proportion (e.g., $\frac{AB}{DE} = \frac{AC}{DF}$ and $\angle A = \angle D$), then the triangles are similar.
- SSS (Side-Side-Side) Similarity: If the corresponding sides of two triangles are in proportion (e.g., $\frac{AB}{DE} = \frac{BC}{EF} = \frac{AC}{DF}$), then the triangles are similar.
Another critical theorem extensively covered is the Basic Proportionality Theorem (BPT), also known as Thales Theorem, and its converse. The BPT states that if a line is drawn parallel to one side of a triangle intersecting the other two sides in distinct points, then the other two sides are divided in the same ratio (e.g., if $DE \parallel BC$ in $\triangle ABC$, then $\frac{AD}{DB} = \frac{AE}{EC}$). The solutions tackle problems where applying the BPT or its converse involves multiple steps or requires combining it with other geometric principles. Closely related, and often proven using similarity, is the theorem regarding the areas of similar triangles: the ratio of the areas of two similar triangles is equal to the square of the ratio of their corresponding sides. That is, if $\triangle ABC \sim \triangle DEF$, then $\frac{\text{ar}(\triangle ABC)}{\text{ar}(\triangle DEF)} = (\frac{AB}{DE})^2 = (\frac{BC}{EF})^2 = (\frac{AC}{DF})^2$. The Exemplar problems frequently leverage this theorem for complex area comparisons or to find side ratios when area ratios are known.
The timeless Pythagoras Theorem ($a^2 + b^2 = c^2$ for a right triangle with legs $a, b$ and hypotenuse $c$) and its converse form the final major pillar of this chapter's Exemplar solutions. Often, the proof of the theorem itself utilizes concepts of triangle similarity. The solutions demonstrate the rigorous application of this theorem and its converse to solve challenging problems. These often involve right-angled triangles embedded within more complex figures, requiring the calculation of lengths, altitudes, or proving specific geometric relationships. Success frequently hinges on employing strategic constructions or skillfully combining the Pythagoras theorem with similarity criteria or the BPT.
These solutions address the full spectrum of Exemplar question formats, from conceptual MCQs and precise Fill-in-the-Blanks/True/False statements to demanding Short and Long Answer questions requiring well-structured, logically sound proofs with explicit justification citing relevant theorems, or multi-step solutions to complex geometric calculations. With clear diagrams, methodical arguments, and precise theorem application highlighted throughout, this resource is indispensable for students seeking to achieve mastery over advanced triangle geometry and excel in rigorous mathematical assessments.
Sample Question 1 & 2 (Before Exercise 6.1)
Choose the correct answer from the given four options:
Sample Question 1: If in Fig 6.1, O is the point of intersection of two chords AB and CD such that OB = OD, then triangles OAC and ODB are
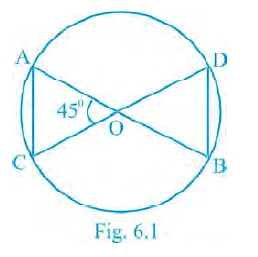
(A) equilateral but not similar
(B) isosceles but not similar
(C) equilateral and similar
(D) isosceles and similar
Answer:
Given:
In the given figure, O is the point of intersection of two chords AB and CD of a circle.
It is also given that $OB = OD$.
To Find:
The relationship between the triangles $\triangle OAC$ and $\triangle ODB$.
Solution:
First, let's analyze the properties of each triangle separately.
Analysis of $\triangle ODB$:
We are given that two sides of the triangle are equal:
OB = OD
(Given)
A triangle with two equal sides is an isosceles triangle. Therefore, $\triangle ODB$ is an isosceles triangle.
In an isosceles triangle, the angles opposite to the equal sides are also equal.
$\angle OBD = \angle ODB$
... (i)
Analysis of $\triangle OAC$:
We know that angles subtended by the same arc at any point on the remaining part of the circle are equal.
The arc AD subtends the angles $\angle ABD$ (or $\angle OBD$) and $\angle ACD$ (or $\angle OCA$) at the circumference.
$\angle OBD = \angle OCA$
[Angles subtended by the same arc AD]
The arc CB subtends the angles $\angle CDB$ (or $\angle ODB$) and $\angle CAB$ (or $\angle OAC$) at the circumference.
$\angle ODB = \angle OAC$
[Angles subtended by the same arc CB]
From equation (i), we know that $\angle OBD = \angle ODB$. Therefore, we can conclude that:
$\angle OCA = \angle OAC$
In $\triangle OAC$, since two angles are equal, the sides opposite to these angles must also be equal. The side opposite to $\angle OCA$ is OA, and the side opposite to $\angle OAC$ is OC.
$OA = OC$
Therefore, $\triangle OAC$ is also an isosceles triangle.
Checking for Similarity:
Now, let's compare the two triangles, $\triangle OAC$ and $\triangle ODB$, to check if they are similar. We will use the Angle-Angle-Angle (AAA) similarity criterion.
In $\triangle OAC$ and $\triangle ODB$:
$\angle AOC = \angle DOB$
[Vertically opposite angles]
$\angle OAC = \angle ODB$
[Angles subtended by the same arc CB]
$\angle OCA = \angle OBD$
[Angles subtended by the same arc AD]
Since all three corresponding angles of the two triangles are equal, the triangles are similar by the AAA similarity criterion.
$\triangle OAC \sim \triangle ODB$
Conclusion:
We have proved that both triangles, $\triangle OAC$ and $\triangle ODB$, are isosceles and they are also similar to each other.
Therefore, option (D) is the correct choice.
The correct option is (D) isosceles and similar.
Sample Question 2: D and E are respectively the points on the sides AB and AC of a triangle ABC such that AD = 2 cm, BD = 3 cm, BC = 7.5 cm and DE || BC. Then, length of DE (in cm) is
(A) 2.5
(B) 3
(C) 5
(D) 6
Answer:
Given:
A triangle $\triangle ABC$.
D and E are points on the sides AB and AC respectively.
$AD = 2$ cm
$BD = 3$ cm
$BC = 7.5$ cm
The line segment DE is parallel to the side BC ($DE \parallel BC$).
To Find:
The length of the line segment DE.
Solution:
We are given that in $\triangle ABC$, the line segment DE is parallel to the side BC.
Now, let's consider the two triangles, $\triangle ADE$ and $\triangle ABC$.
$\angle DAE = \angle BAC$
[Common angle]
Since $DE \parallel BC$ and AB is a transversal line intersecting them, the corresponding angles are equal.
$\angle ADE = \angle ABC$
[Corresponding angles]
Since two corresponding angles of $\triangle ADE$ and $\triangle ABC$ are equal, the two triangles are similar by the Angle-Angle (AA) similarity criterion.
$\triangle ADE \sim \triangle ABC$
When two triangles are similar, the ratio of their corresponding sides is equal.
$\frac{AD}{AB} = \frac{AE}{AC} = \frac{DE}{BC}$
To find the length of DE, we will use the ratio involving the sides whose lengths are known or can be calculated.
$\frac{AD}{AB} = \frac{DE}{BC}$
First, we need to find the length of the side AB.
$AB = AD + DB$
$AB = 2 \text{ cm} + 3 \text{ cm} = 5 \text{ cm}$
Now, substitute the known values into the proportion:
$\frac{2}{5} = \frac{DE}{7.5}$
To solve for DE, we can rearrange the equation:
$DE = \frac{2 \times 7.5}{5}$
$DE = \frac{15}{5}$
$DE = 3$ cm
Hence, the length of DE is 3 cm.
Comparing this result with the given options, we find that option (B) is correct.
Exercise 6.1
Choose the correct answer from the given four options:
Question 1. In Fig. 6.2, ∠BAC = 90° and AD ⊥ BC. Then
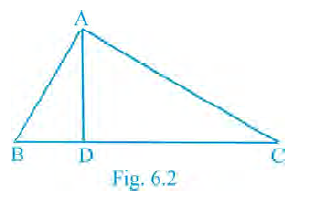
(A) BD . CD = BC2
(B) AB . AC = BC2
(C) BD . CD = AD2
(D) AB . AC = AD2
Answer:
Given:
In the given figure, we have a triangle $\triangle ABC$ where the angle at vertex A is a right angle, i.e., $\angle BAC = 90^\circ$.
A line segment AD is drawn from the vertex A such that it is perpendicular to the opposite side BC, i.e., $AD \perp BC$.
To Find:
The correct relationship among the given options.
Solution:
We know a theorem related to right-angled triangles which states: "If a perpendicular is drawn from the vertex of the right angle of a right triangle to the hypotenuse, then the triangles on both sides of the perpendicular are similar to the whole triangle and to each other."
According to this theorem, the altitude AD divides the triangle $\triangle ABC$ into two smaller triangles, $\triangle ADB$ and $\triangle ADC$, which are similar to each other.
So, we have the similarity relationship:
$\triangle ADB \sim \triangle CDA$
Let's prove this similarity to be sure.
In $\triangle ABC$, since $\angle A = 90^\circ$, we have $\angle B + \angle C = 90^\circ$.
In the right-angled triangle $\triangle ADB$ ($\angle D = 90^\circ$), we have:
$\angle B + \angle BAD = 90^\circ$
... (i)
In the right-angled triangle $\triangle ADC$ ($\angle D = 90^\circ$), we have:
$\angle C + \angle CAD = 90^\circ$
... (ii)
Also, we know that $\angle BAC = \angle BAD + \angle CAD = 90^\circ$.
From equation (i), we can write $\angle B = 90^\circ - \angle BAD$. Since $90^\circ - \angle BAD = \angle CAD$, we get $\angle B = \angle CAD$.
Similarly, from equation (ii), we can write $\angle C = 90^\circ - \angle CAD$. Since $90^\circ - \angle CAD = \angle BAD$, we get $\angle C = \angle BAD$.
Now, in triangles $\triangle ADB$ and $\triangle CDA$:
$\angle ADB = \angle CDA$
(Each $90^\circ$)
$\angle ABD = \angle CAD$
(Proved above)
Therefore, by the Angle-Angle (AA) similarity criterion, the triangles are similar: $\triangle ADB \sim \triangle CDA$.
When two triangles are similar, the ratio of their corresponding sides is equal.
$\frac{AD}{CD} = \frac{DB}{DA} = \frac{AB}{CA}$
Taking the first two parts of the proportion, we get:
$\frac{AD}{CD} = \frac{BD}{AD}$
By cross-multiplication, we get:
$AD \times AD = BD \times CD$
$AD^2 = BD \cdot CD$
This result is also known as the Geometric Mean Theorem or the Altitude Theorem.
Comparing this result with the given options:
(A) BD . CD = BC2 (Incorrect)
(B) AB . AC = BC2 (Incorrect)
(C) BD . CD = AD2 (Correct)
(D) AB . AC = AD2 (Incorrect)
Hence, the correct option is (C).
Question 2. The lengths of the diagonals of a rhombus are 16 cm and 12 cm. Then, the length of the side of the rhombus is
(A) 9 cm
(B) 10 cm
(C) 8 cm
(D) 20 cm
Answer:
Given:
A rhombus with diagonals of length 16 cm and 12 cm.
To Find:
The length of the side of the rhombus.
Solution:
Let the rhombus be ABCD, and let its diagonals AC and BD intersect at the point O.
We are given the lengths of the diagonals:
$AC = 16$ cm
$BD = 12$ cm
We know two important properties of the diagonals of a rhombus:
1. The diagonals bisect each other. This means they cut each other into two equal halves at their point of intersection.
2. The diagonals are perpendicular to each other. This means they intersect at a right angle ($90^\circ$).
Using the first property, we can find the lengths of the segments of the diagonals:
$AO = OC = \frac{AC}{2} = \frac{16}{2} = 8$ cm
$BO = OD = \frac{BD}{2} = \frac{12}{2} = 6$ cm
Using the second property, we know that the angle at the intersection is $90^\circ$.
$\angle AOB = 90^\circ$
Now, let's consider the triangle $\triangle AOB$. It is a right-angled triangle with the right angle at O. The sides OA and OB are the two legs, and the side AB (which is also the side of the rhombus) is the hypotenuse.
By applying the Pythagorean theorem to $\triangle AOB$, we have:
$(\text{Hypotenuse})^2 = (\text{Leg 1})^2 + (\text{Leg 2})^2$
$AB^2 = AO^2 + BO^2$
Substituting the values we found:
$AB^2 = (8)^2 + (6)^2$
$AB^2 = 64 + 36$
$AB^2 = 100$
$AB = \sqrt{100}$
$AB = 10$ cm
Since all sides of a rhombus are equal, the length of the side of the rhombus is 10 cm.
Hence, the correct option is (B).
Question 3. If Δ ABC ~ Δ EDF and Δ ABC is not similar to Δ DEF, then which of the following is not true?
(A) BC . EF = AC. FD
(B) AB . EF = AC . DE
(C) BC . DE = AB . EF
(D) BC . DE = AB . FD
Answer:
Given:
Two triangles are similar with a specific correspondence: $\triangle ABC \sim \triangle EDF$.
It is also mentioned that $\triangle ABC$ is not similar to $\triangle DEF$ to ensure we use the correct vertex correspondence.
To Find:
Which of the given statements is not true based on the given similarity.
Solution:
The statement that the two triangles are similar, $\triangle ABC \sim \triangle EDF$, implies that their corresponding angles are equal and the ratio of their corresponding sides is also equal.
The correspondence between the vertices is as follows:
$A \leftrightarrow E$
$B \leftrightarrow D$
$C \leftrightarrow F$
Based on this correspondence, the ratio of the corresponding sides will be:
$\frac{AB}{ED} = \frac{BC}{DF} = \frac{AC}{EF}$
... (i)
Now, we will check each of the given options by cross-multiplying the parts of this proportion.
(A) BC . EF = AC . FD
Let's consider the second and third parts of the proportion from equation (i):
$\frac{BC}{DF} = \frac{AC}{EF}$
By cross-multiplying, we get:
$BC \cdot EF = AC \cdot DF$
Since $DF$ is the same as $FD$, this statement is identical to the one in option (A). Therefore, option (A) is true.
(B) AB . EF = AC . DE
Let's consider the first and third parts of the proportion from equation (i):
$\frac{AB}{ED} = \frac{AC}{EF}$
By cross-multiplying, we get:
$AB \cdot EF = AC \cdot ED$
Since $ED$ is the same as $DE$, this statement is identical to the one in option (B). Therefore, option (B) is true.
(D) BC . DE = AB . FD
Let's consider the first and second parts of the proportion from equation (i):
$\frac{AB}{ED} = \frac{BC}{DF}$
By cross-multiplying, we get:
$AB \cdot DF = BC \cdot ED$
Since $ED$ is the same as $DE$ and $DF$ is the same as $FD$, this statement is identical to the one in option (D). Therefore, option (D) is true.
(C) BC . DE = AB . EF
This statement can be rewritten in a ratio form as:
$\frac{BC}{EF} = \frac{AB}{DE}$
Let's check if this is consistent with our original proportion from equation (i): $\frac{AB}{ED} = \frac{BC}{DF}$.
The expression in option (C) would be true only if $EF = DF$. This is not generally true for a triangle unless it is an isosceles triangle with specific properties. Since we cannot assume this, the statement in option (C) is derived from an incorrect correspondence of sides.
Therefore, option (C) is not true.
Question 4. If in two triangles ABC and PQR, $\frac{AB}{QR}$ = $\frac{BC}{PR}$ = $\frac{CA}{PQ}$, then,
(A) ΔPQR ~ ΔCAB
(B) ΔPQR ~ ΔABC
(C) ΔCBA ~ ΔPQR
(D) ΔBCA ~ ΔPQR
Answer:
Given:
Two triangles, $\triangle ABC$ and $\triangle PQR$.
The ratio of their sides is given as:
$\frac{AB}{QR} = \frac{BC}{PR} = \frac{CA}{PQ}$
To Find:
The correct similarity statement among the given options.
Solution:
According to the Side-Side-Side (SSS) similarity criterion, if the corresponding sides of two triangles are in the same ratio, then the triangles are similar.
To determine the correct similarity statement, we need to establish the correspondence between the vertices of the two triangles using the given ratio of sides.
The vertex opposite a given side in one triangle corresponds to the vertex opposite the corresponding side in the other triangle.
Let's analyze the given ratio part by part:
1. From the ratio $\frac{AB}{QR}$, we see that side AB of $\triangle ABC$ corresponds to side QR of $\triangle PQR$.
- The vertex opposite to side AB in $\triangle ABC$ is C.
- The vertex opposite to side QR in $\triangle PQR$ is P.
- Therefore, the vertex C corresponds to P ($C \leftrightarrow P$).
2. From the ratio $\frac{BC}{PR}$, we see that side BC of $\triangle ABC$ corresponds to side PR of $\triangle PQR$.
- The vertex opposite to side BC in $\triangle ABC$ is A.
- The vertex opposite to side PR in $\triangle PQR$ is Q.
- Therefore, the vertex A corresponds to Q ($A \leftrightarrow Q$).
3. From the ratio $\frac{CA}{PQ}$, we see that side CA of $\triangle ABC$ corresponds to side PQ of $\triangle PQR$.
- The vertex opposite to side CA in $\triangle ABC$ is B.
- The vertex opposite to side PQ in $\triangle PQR$ is R.
- Therefore, the vertex B corresponds to R ($B \leftrightarrow R$).
So, we have the following correspondence between the vertices:
$A \leftrightarrow Q$
$B \leftrightarrow R$
$C \leftrightarrow P$
Based on this correspondence, we can write the similarity statement as $\triangle ABC \sim \triangle QRP$.
Now, let's check the given options to find the one that matches this correspondence:
(A) $\triangle PQR \sim \triangle CAB$
This statement implies the correspondence:
$P \leftrightarrow C$, $Q \leftrightarrow A$, $R \leftrightarrow B$.
This is the exact same correspondence we derived. Therefore, this statement is correct.
(B) $\triangle PQR \sim \triangle ABC$
This implies $P \leftrightarrow A$, $Q \leftrightarrow B$, $R \leftrightarrow C$. This is incorrect.
(C) $\triangle CBA \sim \triangle PQR$
This implies $C \leftrightarrow P$, $B \leftrightarrow Q$, $A \leftrightarrow R$. This is incorrect.
(D) $\triangle BCA \sim \triangle PQR$
This implies $B \leftrightarrow P$, $C \leftrightarrow Q$, $A \leftrightarrow R$. This is incorrect.
Hence, the correct option is (A).
Question 5. In Fig.6.3, two line segments AC and BD intersect each other at the point P such that PA = 6 cm, PB = 3 cm, PC = 2.5 cm, PD = 5 cm, ∠APB = 50° and ∠CDP = 30°. Then, ∠PBA is equal to
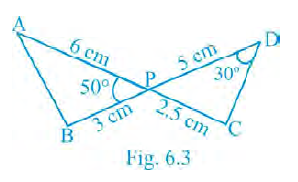
(A) 50°
(B) 30°
(C) 60°
(D) 100°
Answer:
Given:
Two line segments AC and BD intersect at point P.
The lengths of the segments are:
$PA = 6$ cm, $PB = 3$ cm, $PC = 2.5$ cm, and $PD = 5$ cm.
The angles are:
$\angle APB = 50^\circ$ and $\angle CDP = 30^\circ$.
To Find:
The measure of the angle $\angle PBA$.
Solution:
We will check if the two triangles formed by the intersecting lines, $\triangle PAB$ and $\triangle PDC$, are similar.
First, let's compare the angles at the point of intersection P.
$\angle APB$ and $\angle DPC$ are vertically opposite angles. Therefore, they are equal.
$\angle DPC = \angle APB = 50^\circ$
[Vertically opposite angles]
Now, let's check the ratio of the sides that include these angles.
Let's calculate the ratio of the sides of $\triangle PAB$ to the sides of $\triangle PDC$. We can form the ratios in two ways. Let's try matching the sides PA with PD and PB with PC.
Ratio 1: $\frac{PA}{PD} = \frac{6}{5}$
Ratio 2: $\frac{PB}{PC} = \frac{3}{2.5} = \frac{30}{25} = \frac{6}{5}$
Since the ratios are equal, we have:
$\frac{PA}{PD} = \frac{PB}{PC}$
We have now shown that two pairs of sides of the triangles $\triangle PAB$ and $\triangle PDC$ are in proportion, and the angle included between these sides is equal ($\angle APB = \angle DPC$).
Therefore, by the Side-Angle-Side (SAS) similarity criterion, the two triangles are similar.
The correct similarity correspondence is based on the proportional sides: the vertex between sides PA and PB (vertex A) corresponds to the vertex between sides PD and PC (vertex D). So, the similarity is:
$\triangle PAB \sim \triangle PDC$
When two triangles are similar, their corresponding angles are equal.
The correspondence of angles is as follows:
$\angle PAB = \angle PDC$ (also known as $\angle CDP$)
$\angle PBA = \angle PCD$
$\angle APB = \angle DPC$
We are given that $\angle CDP = 30^\circ$. Therefore,
$\angle PAB = 30^\circ$
Now, we can find the required angle $\angle PBA$ by applying the angle sum property to the triangle $\triangle PAB$. The sum of the interior angles of a triangle is $180^\circ$.
In $\triangle PAB$:
$\angle PBA + \angle PAB + \angle APB = 180^\circ$
Substituting the known values:
$\angle PBA + 30^\circ + 50^\circ = 180^\circ$
$\Rightarrow \angle PBA + 80^\circ = 180^\circ$
$\Rightarrow \angle PBA = 180^\circ - 80^\circ$
$\Rightarrow \angle PBA = 100^\circ$
Hence, the correct option is (D) 100°.
Question 6. If in two triangles DEF and PQR, ∠D = ∠Q and ∠R = ∠E, then which of the following is not true?
(A) $\frac{EF}{PR}$ = $\frac{DF}{PQ}$
(B) $\frac{DE}{PQ}$ = $\frac{EF}{RP}$
(C) $\frac{DE}{QR}$ = $\frac{DE}{PQ}$
(D) $\frac{EF}{RP}$ = $\frac{DE}{QR}$
Answer:
Given:
Two triangles, $\triangle DEF$ and $\triangle PQR$.
The angles are related as follows:
$\angle D = \angle Q$
$\angle R = \angle E$
To Find:
Which of the given statements about the ratio of sides is not true.
Solution:
First, we need to establish the similarity between the two triangles.
We are given that two pairs of corresponding angles are equal:
$\angle D = \angle Q$
(Given)
$\angle E = \angle R$
(Given)
Since the sum of angles in any triangle is $180^\circ$, if two angles are equal, the third angle must also be equal.
In $\triangle DEF$, $\angle F = 180^\circ - (\angle D + \angle E)$.
In $\triangle PQR$, $\angle P = 180^\circ - (\angle Q + \angle R)$.
Since $\angle D = \angle Q$ and $\angle E = \angle R$, it follows that $\angle F = \angle P$.
Therefore, by the Angle-Angle-Angle (AAA) similarity criterion (or simply the AA criterion), the two triangles are similar.
To write the correct similarity statement, we need to match the corresponding vertices based on the equal angles:
$D \leftrightarrow Q$
$E \leftrightarrow R$
$F \leftrightarrow P$
The correct similarity statement is:
$\triangle DEF \sim \triangle QRP$
When two triangles are similar, the ratio of their corresponding sides is equal. The corresponding sides are those opposite to the equal angles.
$\frac{DE}{QR} = \frac{EF}{RP} = \frac{DF}{QP}$
Now, we will check each of the given options against this correct proportion.
(A) $\frac{EF}{PR} = \frac{DF}{PQ}$
This matches the second and third parts of our derived proportion ($\frac{EF}{RP} = \frac{DF}{QP}$). Therefore, option (A) is true.
(C) $\frac{DE}{QR} = \frac{DF}{PQ}$
This matches the first and third parts of our derived proportion ($\frac{DE}{QR} = \frac{DF}{QP}$). Therefore, option (C) is true.
(D) $\frac{EF}{RP} = \frac{DE}{QR}$
This matches the first and second parts of our derived proportion. Therefore, option (D) is true.
(B) $\frac{DE}{PQ} = \frac{EF}{RP}$
Let's examine this statement. It compares the ratio of DE to PQ with the ratio of EF to RP. According to our correct proportion, $\frac{DE}{QR} = \frac{EF}{RP}$. The statement in option (B) would only be true if $PQ = QR$. This is not generally true for a triangle unless it is isosceles. Since we cannot assume this, the statement in option (B) is based on an incorrect correspondence of sides (it incorrectly pairs side DE with PQ).
Therefore, option (B) is not true.
Question 7. In triangles ABC and DEF, ∠B = ∠E, ∠F =∠C and AB = 3 DE. Then, the two triangles are
(A) congruent but not similar
(B) similar but not congruent
(C) neither congruent nor similar
(D) congruent as well as similar
Given:
In triangles ABC and DEF:
$\angle B = \angle E$
$\angle C = \angle F$
$AB = 3 DE$
To Find:
The relationship between the two triangles (similar, congruent, both, or neither).
Solution:
First, we check for similarity.
In $\triangle ABC$ and $\triangle DEF$, we are given that two pairs of corresponding angles are equal:
$\angle B = \angle E$
(Given)
$\angle C = \angle F$
(Given)
By the Angle-Angle (AA) similarity criterion, if two angles of one triangle are equal to two corresponding angles of another triangle, then the two triangles are similar.
Since the sum of angles in a triangle is $180^\circ$, the third pair of angles must also be equal, i.e., $\angle A = \angle D$.
The correspondence of vertices is A $\leftrightarrow$ D, B $\leftrightarrow$ E, and C $\leftrightarrow$ F. Thus, the similarity is correctly stated as $\triangle ABC \sim \triangle DEF$. So, the triangles are similar.
Next, we check for congruence.
For two triangles to be congruent, they must have the same shape and size. This means they must be similar, and the ratio of their corresponding sides must be equal to 1.
Let's find the ratio of the corresponding sides AB and DE.
We are given the relationship:
$AB = 3 DE$
Dividing both sides by DE, we get the ratio:
$\frac{AB}{DE} = 3$
Since the ratio of corresponding sides is 3, which is not equal to 1, the triangles are of different sizes.
Therefore, the triangles are not congruent.
Conclusion: The two triangles are similar but not congruent.
The correct option is (B) similar but not congruent.
Question 8. It is given that ΔABC ~ ΔPQR, with $\frac{BC}{QR}$ = $\frac{1}{3}$ . Then, $\frac{ar (PRQ)}{ar (BCA)}$ is equal to
(A) 9
(B) 3
(C) $\frac{1}{3}$
(D) $\frac{1}{9}$
Given:
It is given that $\triangle ABC \sim \triangle PQR$.
The ratio of corresponding sides is given as $\frac{BC}{QR} = \frac{1}{3}$.
To Find:
The value of the ratio $\frac{ar (PRQ)}{ar (BCA)}$.
Solution:
We know the theorem: "The ratio of the areas of two similar triangles is equal to the square of the ratio of their corresponding sides."
Since it is given that $\triangle ABC \sim \triangle PQR$, the ratio of their areas is:
$\frac{ar (ABC)}{ar (PQR)} = \left(\frac{AB}{PQ}\right)^2 = \left(\frac{BC}{QR}\right)^2 = \left(\frac{AC}{PR}\right)^2$
We are given the ratio of the corresponding sides BC and QR:
$\frac{BC}{QR} = \frac{1}{3}$
Substituting this value into the area ratio formula, we get:
$\frac{ar (ABC)}{ar (PQR)} = \left(\frac{1}{3}\right)^2 = \frac{1}{9}$
We need to find the value of $\frac{ar (PRQ)}{ar (BCA)}$.
The area of a triangle is independent of the order in which its vertices are named. Therefore, $ar(PRQ) = ar(PQR)$ and $ar(BCA) = ar(ABC)$.
So, we need to find $\frac{ar (PQR)}{ar (ABC)}$.
This is the reciprocal of the ratio we just calculated.
$\frac{ar (PQR)}{ar (ABC)} = \frac{1}{\left(\frac{ar (ABC)}{ar (PQR)}\right)} = \frac{1}{\frac{1}{9}} = 9$
Therefore, $\frac{ar (PRQ)}{ar (BCA)} = 9$.
Conclusion:
The correct option is (A) 9.
Question 9. It is given that ΔABC ~ ΔDFE,∠A = 30°∠C = 50°, AB = 5 cm, AC = 8 cm and DF = 7.5 cm. Then, the following is true:
(A) DE = 12 cm,∠F = 50°
(B) DE = 12 cm, ∠F = 100°
(C) EF = 12 cm, ∠D = 100°
(D) EF = 12 cm, ∠D = 30°
Given:
$\triangle ABC \sim \triangle DFE$
$\angle A = 30^\circ$, $\angle C = 50^\circ$
$AB = 5$ cm, $AC = 8$ cm, $DF = 7.5$ cm
To Find:
Which of the given statements is true.
Solution:
Step 1: Find the angles.
Since $\triangle ABC \sim \triangle DFE$, their corresponding angles are equal. The correspondence is:
$A \leftrightarrow D$, $B \leftrightarrow F$, $C \leftrightarrow E$.
Therefore:
$\angle D = \angle A = 30^\circ$
$\angle E = \angle C = 50^\circ$
First, find $\angle B$ in $\triangle ABC$ using the angle sum property:
$\angle B = 180^\circ - (\angle A + \angle C) = 180^\circ - (30^\circ + 50^\circ) = 180^\circ - 80^\circ = 100^\circ$.
Since $\angle F$ corresponds to $\angle B$, we have:
$\angle F = \angle B = 100^\circ$.
Step 2: Find the side lengths.
Since the triangles are similar, the ratio of their corresponding sides is equal:
$\frac{AB}{DF} = \frac{BC}{FE} = \frac{AC}{DE}$
Substitute the given values into this proportion:
$\frac{5}{7.5} = \frac{BC}{FE} = \frac{8}{DE}$
Let's calculate the ratio from the known sides:
$\frac{5}{7.5} = \frac{50}{75} = \frac{2}{3}$
Now we can use this ratio to find the length of DE:
$\frac{AC}{DE} = \frac{2}{3}$
$\frac{8}{DE} = \frac{2}{3}$
Cross-multiplying gives:
$2 \times DE = 8 \times 3$
$2 \times DE = 24$
$DE = \frac{24}{2} = 12$ cm.
Step 3: Check the options.
We have found that $DE = 12$ cm and the angles are $\angle D = 30^\circ$, $\angle E = 50^\circ$, and $\angle F = 100^\circ$.
(A) DE = 12 cm, $\angle F = 50^\circ$. (Incorrect, $\angle F$ is $100^\circ$)
(B) DE = 12 cm, $\angle F = 100^\circ$. (Correct)
(C) EF = 12 cm, $\angle D = 100^\circ$. (Incorrect, $DE = 12$ cm and $\angle D$ is $30^\circ$)
(D) EF = 12 cm, $\angle D = 30^\circ$. (Incorrect, $DE = 12$ cm)
Conclusion:
The correct option is (B) DE = 12 cm, ∠F = 100°.
Question 10. If in triangles ABC and DEF, $\frac{AB}{DE}$ = $\frac{BC}{FD}$ , then they will be similar, when
(A) ∠B = ∠E
(B) ∠A = ∠D
(C) ∠B = ∠D
(D) ∠A = ∠F
Given:
In two triangles, $\triangle ABC$ and $\triangle DEF$, the ratio of two pairs of sides is equal:
$\frac{AB}{DE} = \frac{BC}{FD}$
To Find:
The condition that will make the two triangles similar.
Solution:
We can use the Side-Angle-Side (SAS) similarity criterion to determine the condition for similarity.
The SAS criterion states that if an angle of one triangle is equal to an angle of another triangle and the sides including these angles are in the same ratio, then the triangles are similar.
Let's identify the included angles for the given sides:
1. In $\triangle ABC$, the given sides are AB and BC. The angle included between these two sides is $\angle B$.
2. In $\triangle DEF$, the corresponding sides given in the ratio are DE and FD. The angle included between these two sides is $\angle D$.
For the triangles to be similar by the SAS criterion, the included angles must be equal.
Therefore, the required condition is:
$\angle B = \angle D$
If this condition holds, the similarity correspondence will be $\triangle ABC \sim \triangle EDF$, and the ratio of sides will be $\frac{AB}{ED} = \frac{BC}{DF} = \frac{AC}{EF}$, which is consistent with the given information.
Conclusion:
The triangles will be similar when the included angles are equal, which means $\angle B = \angle D$.
The correct option is (C) ∠B = ∠D.
Question 11. If ΔABC ~ ΔQRP, $\frac{ar (ABC)}{ar (PQR)}$ = $\frac{9}{4}$ , AB = 18 cm and BC = 15 cm, then PR is equal to
(A) 10 cm
(B) 12 cm
(C) $\frac{20}{3}$ cm
(D) 8 cm
Given:
$\triangle ABC \sim \triangle QRP$
$\frac{ar (ABC)}{ar (PQR)} = \frac{9}{4}$
$BC = 15$ cm
(AB = 18 cm is also given, but may not be needed).
To Find:
The length of the side PR.
Solution:
We use the theorem stating that the ratio of the areas of two similar triangles is equal to the square of the ratio of their corresponding sides.
The given similarity is $\triangle ABC \sim \triangle QRP$. This establishes the correspondence between vertices:
$A \leftrightarrow Q$, $B \leftrightarrow R$, $C \leftrightarrow P$.
Therefore, the corresponding sides are AB with QR, BC with RP, and AC with QP.
The ratio of areas can be written as:
$\frac{ar (ABC)}{ar (QRP)} = \left(\frac{BC}{RP}\right)^2$
We are given $\frac{ar (ABC)}{ar (PQR)} = \frac{9}{4}$. Since the area is independent of vertex order, $ar(PQR) = ar(QRP)$.
Substituting the given values into our area ratio equation:
$\frac{9}{4} = \left(\frac{15}{PR}\right)^2$
To find the ratio of the sides, we take the square root of both sides:
$\sqrt{\frac{9}{4}} = \frac{15}{PR}$
$\frac{3}{2} = \frac{15}{PR}$
Now, we can solve for PR by cross-multiplication:
$3 \times PR = 2 \times 15$
$3 \times PR = 30$
$PR = \frac{30}{3} = 10$ cm
Conclusion:
The length of PR is 10 cm.
The correct option is (A) 10 cm.
Question 12. If S is a point on side PQ of a ΔPQR such that PS = QS = RS, then
(A) PR . QR = RS2
(B) QS2 + RS2 = QR2
(C) PR2 + QR2 = PQ2
(D) PS2 + RS2 = PR2
Given:
In $\triangle PQR$, S is a point on the side PQ such that $PS = QS = RS$.
To Find:
The correct relationship among the given options.
Solution:
The condition $PS = QS$ means that S is the midpoint of the side PQ.
The condition $PS = QS = RS$ means that the point S is equidistant from all three vertices P, Q, and R of the triangle.
The point that is equidistant from all three vertices of a triangle is the circumcenter, which is the center of the circle that passes through all three vertices (the circumcircle).
In this case, the circumcenter S lies on one of the sides of the triangle (the side PQ). This can only happen if that side is the diameter of the circumcircle.
If PQ is the diameter of the circumcircle, then the angle subtended by the diameter at any point on the circumference is a right angle ($90^\circ$). The angle opposite to the diameter PQ is $\angle PRQ$.
Therefore, $\triangle PQR$ is a right-angled triangle with the right angle at vertex R.
$\angle PRQ = 90^\circ$
Now, we can apply the Pythagorean theorem to the right-angled triangle PQR. The theorem states that the square of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the other two sides.
The hypotenuse is PQ, and the other two sides are PR and QR.
So, we have the relationship:
$PR^2 + QR^2 = PQ^2$
Conclusion:
The correct statement describing the relationship between the sides of the triangle is $PR^2 + QR^2 = PQ^2$.
The correct option is (C) PR2 + QR2 = PQ2.
Sample Question 1 to 3 (Before Exercise 6.2)
Sample Question 1: In ΔABC, AB = 24 cm, BC = 10 cm and AC = 26 cm. Is this triangle a right triangle? Give reasons for your answer.
Given:
The lengths of the sides of a triangle $\triangle ABC$ are:
$AB = 24$ cm
$BC = 10$ cm
$AC = 26$ cm
To Determine:
Whether $\triangle ABC$ is a right triangle or not, with justification.
Solution:
To determine if the given triangle is a right triangle, we can use the Converse of the Pythagorean Theorem. This theorem states that if the square of the length of the longest side of a triangle is equal to the sum of the squares of the lengths of the other two sides, then the triangle is a right-angled triangle.
First, we identify the longest side. Comparing the lengths $24$ cm, $10$ cm, and $26$ cm, the longest side is $AC = 26$ cm. If the triangle is a right triangle, this side would be the hypotenuse.
Now, let's calculate the square of the longest side:
$AC^2 = (26)^2 = 676$
Next, we calculate the sum of the squares of the other two sides:
$AB^2 + BC^2 = (24)^2 + (10)^2$
$AB^2 + BC^2 = 576 + 100$
$AB^2 + BC^2 = 676$
Now, we compare the two results:
$AC^2 = 676$
$AB^2 + BC^2 = 676$
Since $AC^2 = AB^2 + BC^2$, the condition of the Converse of the Pythagorean Theorem is satisfied.
Conclusion:
Yes, the triangle ABC is a right triangle.
The reason is that the sides of the triangle satisfy the condition of the Converse of the Pythagorean Theorem. The angle opposite the longest side (AC), which is $\angle B$, is the right angle ($\angle B = 90^\circ$).
Sample Question 2: P and Q are the points on the sides DE and DF of a triangle DEF such that DP = 5 cm, DE = 15 cm, DQ= 6 cm and QF = 18 cm. Is PQ || EF? Give reasons for your answer
Given:
In a triangle $\triangle DEF$, P is a point on side DE and Q is a point on side DF.
$DP = 5$ cm
$DE = 15$ cm
$DQ = 6$ cm
$QF = 18$ cm
To Determine:
Whether the line segment PQ is parallel to the side EF (PQ || EF), with justification.
Solution:
To determine if PQ is parallel to EF, we use the Converse of the Basic Proportionality Theorem (BPT). This theorem states that if a line divides any two sides of a triangle in the same ratio, then the line is parallel to the third side.
We need to check if the line segment PQ divides the sides DE and DF in the same ratio. That is, we need to check if $\frac{DP}{PE} = \frac{DQ}{QF}$.
First, we need to find the length of the segment PE. Since P is on DE, the length of PE is the total length of DE minus the length of DP.
$PE = DE - DP$
$PE = 15 \text{ cm} - 5 \text{ cm} = 10$ cm
Now, we calculate the ratio on the side DE:
$\frac{DP}{PE} = \frac{5}{10} = \frac{1}{2}$
Next, we calculate the ratio on the side DF. We are given the lengths of DQ and QF directly.
$\frac{DQ}{QF} = \frac{6}{18} = \frac{1}{3}$
Now, we compare the two ratios:
We find that $\frac{1}{2} \neq \frac{1}{3}$.
Therefore, $\frac{DP}{PE} \neq \frac{DQ}{QF}$.
Conclusion:
No, the line segment PQ is not parallel to the side EF.
The reason is that the line PQ does not divide the sides DE and DF in the same ratio. Since the condition for the Converse of the Basic Proportionality Theorem is not met, we conclude that PQ is not parallel to EF.
Sample Question 3: It is given that Δ FED ~ Δ STU . Is it true to say that $\frac{DE}{ST}$ = $\frac{EF}{TU}$ ? Why?
Given:
Two triangles, $\triangle FED$ and $\triangle STU$, are similar. The similarity statement is given as $\triangle FED \sim \triangle STU$.
To Determine:
Whether the statement $\frac{DE}{ST} = \frac{EF}{TU}$ is true, with justification.
Solution:
When two triangles are declared similar, the order of the vertices in the similarity statement is very important because it defines the correspondence between the vertices, angles, and sides of the two triangles.
The given similarity statement is $\triangle FED \sim \triangle STU$.
This implies the following correspondence between the vertices:
$F \leftrightarrow S$
$E \leftrightarrow T$
$D \leftrightarrow U$
Based on this vertex correspondence, we can identify the corresponding sides. A side is formed by two vertices, so the corresponding side in the second triangle is formed by the corresponding two vertices.
Side FE corresponds to side ST.
Side ED corresponds to side TU.
Side DF corresponds to side US.
For similar triangles, the ratio of the lengths of corresponding sides is equal. Therefore, the correct proportion is:
$\frac{FE}{ST} = \frac{ED}{TU} = \frac{DF}{US}$
Let's rewrite this using the side names from the question: $\frac{EF}{ST} = \frac{DE}{TU}$.
Now let's examine the statement we are asked to verify: $\frac{DE}{ST} = \frac{EF}{TU}$.
In this statement, the side DE from the first triangle is being compared with the side ST from the second triangle. However, the correct corresponding side for DE is TU.
Similarly, the side EF from the first triangle is being compared with the side TU from the second triangle. However, the correct corresponding side for EF is ST.
The given statement has incorrectly matched the sides. It has swapped the denominators compared to the correct proportion derived from the similarity statement.
Conclusion:
No, the statement is false.
Reason: The ratio of corresponding sides must be based on the correct vertex correspondence given by the similarity statement $\triangle FED \sim \triangle STU$. According to this correspondence, the side DE corresponds to the side TU, and the side EF corresponds to the side ST. Therefore, the correct equality of ratios is $\frac{DE}{TU} = \frac{EF}{ST}$, not $\frac{DE}{ST} = \frac{EF}{TU}$.
Exercise 6.2
Question 1. Is the triangle with sides 25 cm, 5 cm and 24 cm a right triangle? Give reasons for your answer.
Given:
A triangle with side lengths 25 cm, 5 cm, and 24 cm.
To Determine:
Whether the triangle is a right triangle, with proper reasoning.
Solution:
To determine if the triangle is a right triangle, we will use the Converse of the Pythagorean Theorem. This theorem states that if the square of the length of the longest side of a triangle is equal to the sum of the squares of the lengths of the other two sides, then the triangle is a right-angled triangle.
First, we identify the longest side of the triangle. The side lengths are 25 cm, 5 cm, and 24 cm. The longest side is 25 cm. If the triangle is a right triangle, this side must be the hypotenuse.
Now, let's calculate the square of the longest side:
$(25)^2 = 625$
Next, let's calculate the sum of the squares of the other two sides:
$(5)^2 + (24)^2 = 25 + 576 = 601$
We now compare the square of the longest side with the sum of the squares of the other two sides.
$625 \neq 601$
Since the square of the longest side is not equal to the sum of the squares of the other two sides, the triangle does not satisfy the condition of the Converse of the Pythagorean Theorem.
Conclusion:
No, the triangle with sides 25 cm, 5 cm, and 24 cm is not a right triangle.
Reason: The square of the longest side (625) is not equal to the sum of the squares of the other two sides (601). Therefore, the triangle does not satisfy the Converse of the Pythagorean Theorem.
Question 2. It is given that ΔDEF ~ ΔRPQ. Is it true to say that ∠D = ∠R and ∠F = ∠P? Why?
Given:
Two triangles, $\triangle DEF$ and $\triangle RPQ$, are similar. The similarity is stated as $\triangle DEF \sim \triangle RPQ$.
To Determine:
If the statement "$\angle D = \angle R$ and $\angle F = \angle P$" is true, and provide the reason.
Solution:
When two triangles are similar, their corresponding angles are equal. The correspondence between the angles is determined by the order of the vertices in the similarity statement.
For the given similarity statement $\triangle DEF \sim \triangle RPQ$, the correspondence is as follows:
The first vertex of $\triangle DEF$, which is D, corresponds to the first vertex of $\triangle RPQ$, which is R.
The second vertex, E, corresponds to the second vertex, P.
The third vertex, F, corresponds to the third vertex, Q.
This gives us the following set of equal corresponding angles:
$\angle D = \angle R$
$\angle E = \angle P$
$\angle F = \angle Q$
Now, let's examine the statement we need to verify: "$\angle D = \angle R$ and $\angle F = \angle P$".
Comparing this with our derived equalities:
1. The part "$\angle D = \angle R$" is true, as D and R are corresponding vertices.
2. The part "$\angle F = \angle P$" is false. According to the correspondence, $\angle F$ corresponds to $\angle Q$ (so $\angle F = \angle Q$), and $\angle P$ corresponds to $\angle E$ (so $\angle P = \angle E$).
Since one part of the combined statement is false, the entire statement is false.
Conclusion:
No, the statement is false.
Reason: The similarity statement $\triangle DEF \sim \triangle RPQ$ dictates the correspondence of vertices. While it correctly implies that $\angle D = \angle R$, it implies that $\angle F$ corresponds to $\angle Q$ (not $\angle P$) and $\angle E$ corresponds to $\angle P$. Therefore, the correct equalities are $\angle F = \angle Q$ and $\angle E = \angle P$, which contradicts the second part of the given statement.
Question 3. A and B are respectively the points on the sides PQ and PR of a triangle PQR such that PQ = 12.5 cm, PA = 5 cm, BR= 6 cm and PB = 4 cm. Is AB || QR? Give reasons for your answer.
Given:
In $\triangle PQR$, A is a point on side PQ and B is a point on side PR.
$PQ = 12.5$ cm
$PA = 5$ cm
$PB = 4$ cm
$BR = 6$ cm
To Determine:
Whether the line segment AB is parallel to the side QR, with proper reasoning.
Solution:
To determine if AB is parallel to QR, we will use the Converse of the Basic Proportionality Theorem (BPT). This theorem states that if a line divides any two sides of a triangle in the same ratio, then the line is parallel to the third side.
We need to check if the line segment AB divides the sides PQ and PR in the same ratio. That is, we must check if $\frac{PA}{AQ} = \frac{PB}{BR}$.
First, we need to find the length of the segment AQ. Since A is on PQ, the length of AQ is the total length of PQ minus the length of PA.
$AQ = PQ - PA$
$AQ = 12.5 \text{ cm} - 5 \text{ cm} = 7.5$ cm
Now, let's calculate the ratio of the segments on the side PQ:
$\frac{PA}{AQ} = \frac{5}{7.5} = \frac{50}{75} = \frac{2 \times \cancel{25}}{3 \times \cancel{25}} = \frac{2}{3}$
Next, let's calculate the ratio of the segments on the side PR. We are given the lengths of PB and BR directly.
$\frac{PB}{BR} = \frac{4}{6} = \frac{2 \times \cancel{2}}{3 \times \cancel{2}} = \frac{2}{3}$
Now, we compare the two ratios:
The ratio on side PQ is $\frac{PA}{AQ} = \frac{2}{3}$.
The ratio on side PR is $\frac{PB}{BR} = \frac{2}{3}$.
Since the ratios are equal, $\frac{PA}{AQ} = \frac{PB}{BR}$.
Conclusion:
Yes, the line segment AB is parallel to the side QR.
Reason: The line segment AB divides the sides PQ and PR of $\triangle PQR$ in the same ratio ($\frac{2}{3}$). Therefore, by the Converse of the Basic Proportionality Theorem, AB is parallel to QR.
Question 4. In Fig 6.4, BD and CE intersect each other at the point P. Is Δ PBC ~ Δ PDE? Why?
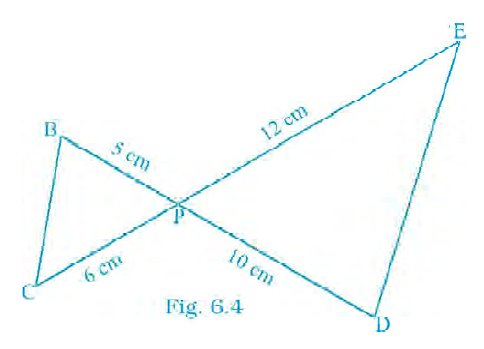
Answer:
Given:
From the given figure, two line segments BD and CE intersect at a point P, forming two triangles, $\triangle PBC$ and $\triangle PDE$.
The lengths of the segments are:
$PB = 5$ cm
$PC = 6$ cm
$PD = 10$ cm
$PE = 12$ cm
To Determine:
Whether $\triangle PBC$ is similar to $\triangle PDE$ ($\triangle PBC \sim \triangle PDE$), and to provide a reason.
Solution:
To determine if the two triangles are similar, we can check if they satisfy the conditions for one of the similarity criteria (AA, SSS, or SAS).
Since we are given the lengths of two sides and can determine the included angle for each triangle, we will use the Side-Angle-Side (SAS) similarity criterion.
The SAS criterion states that if two sides of one triangle are proportional to two sides of another triangle and their included angles are equal, then the two triangles are similar.
Let's consider the triangles $\triangle PBC$ and $\triangle PDE$.
Step 1: Check the included angles.
The angle $\angle BPC$ in $\triangle PBC$ and the angle $\angle DPE$ in $\triangle PDE$ are vertically opposite angles formed by the intersection of lines BD and CE.
Therefore, their measures are equal.
$\angle BPC = \angle DPE$
[Vertically opposite angles]
Step 2: Check the ratio of the sides that include these angles.
For the similarity statement $\triangle PBC \sim \triangle PDE$ to be true, the ratio of corresponding sides must be equal. The correspondence would be P $\leftrightarrow$ P, B $\leftrightarrow$ D, and C $\leftrightarrow$ E.
This means we need to check if $\frac{PB}{PD} = \frac{PC}{PE}$.
Let's calculate the first ratio:
$\frac{PB}{PD} = \frac{5}{10} = \frac{1}{2}$
Now, let's calculate the second ratio:
$\frac{PC}{PE} = \frac{6}{12} = \frac{1}{2}$
The ratios are equal:
$\frac{PB}{PD} = \frac{PC}{PE} = \frac{1}{2}$
Since the ratio of two pairs of corresponding sides is equal and the angles included between these sides are also equal, the condition for SAS similarity is met.
Conclusion:
Yes, the triangles are similar: $\triangle PBC \sim \triangle PDE$.
Reason: The triangles satisfy the SAS similarity criterion. The ratios of the corresponding sides including the angle at P are equal ($\frac{PB}{PD} = \frac{PC}{PE} = \frac{1}{2}$), and their included angles are equal because they are vertically opposite angles ($\angle BPC = \angle DPE$).
Question 5. In triangles PQR and MST, ∠P = 55°, ∠Q = 25°, ∠M = 100° and ∠S = 25°. Is ΔQPR ~ ΔTSM? Why?
Given:
In $\triangle PQR$: $\angle P = 55^\circ$, $\angle Q = 25^\circ$.
In $\triangle MST$: $\angle M = 100^\circ$, $\angle S = 25^\circ$.
To Determine:
Whether the similarity statement $\triangle QPR \sim \triangle TSM$ is true, and provide a reason.
Solution:
First, we find the third angle in each triangle using the Angle Sum Property of a triangle (sum of angles is $180^\circ$).
In $\triangle PQR$:
$\angle R = 180^\circ - (\angle P + \angle Q)$
$\angle R = 180^\circ - (55^\circ + 25^\circ) = 180^\circ - 80^\circ = 100^\circ$
In $\triangle MST$:
$\angle T = 180^\circ - (\angle M + \angle S)$
$\angle T = 180^\circ - (100^\circ + 25^\circ) = 180^\circ - 125^\circ = 55^\circ$
Now, we have all the angles for both triangles:
$\triangle PQR$: $\angle P = 55^\circ$, $\angle Q = 25^\circ$, $\angle R = 100^\circ$
$\triangle MST$: $\angle M = 100^\circ$, $\angle S = 25^\circ$, $\angle T = 55^\circ$
The two triangles are similar because all three of their corresponding angles are equal ($\{55^\circ, 25^\circ, 100^\circ\}$). Now we must check if the given similarity statement $\triangle QPR \sim \triangle TSM$ is correct.
This statement implies the following correspondence of vertices:
$Q \leftrightarrow T$, $P \leftrightarrow S$, $R \leftrightarrow M$
Let's check if the corresponding angles are equal based on this statement:
1. Is $\angle Q = \angle T$? We have $\angle Q = 25^\circ$ and $\angle T = 55^\circ$. Since $25^\circ \neq 55^\circ$, this correspondence is incorrect.
2. Is $\angle P = \angle S$? We have $\angle P = 55^\circ$ and $\angle S = 25^\circ$. Since $55^\circ \neq 25^\circ$, this correspondence is incorrect.
3. Is $\angle R = \angle M$? We have $\angle R = 100^\circ$ and $\angle M = 100^\circ$. This correspondence is correct.
Since not all corresponding angles under the statement $\triangle QPR \sim \triangle TSM$ are equal, the statement is not written correctly.
Conclusion:
No, the statement is false.
Reason: Although the two triangles are similar by the AAA similarity criterion (as they have the same set of angles: $55^\circ, 25^\circ, 100^\circ$), the specific vertex correspondence in the statement $\triangle QPR \sim \triangle TSM$ is incorrect. For this statement to be true, we would need $\angle Q = \angle T$, $\angle P = \angle S$, and $\angle R = \angle M$. However, we found that $\angle Q \neq \angle T$ and $\angle P \neq \angle S$. A correct similarity statement would be $\triangle PQR \sim \triangle TSM$.
Question 6. Is the following statement true? Why?
“Two quadrilaterals are similar, if their corresponding angles are equal”.
Given Statement:
“Two quadrilaterals are similar, if their corresponding angles are equal”.
To Determine:
Whether the given statement is true, with justification.
Solution:
For any two polygons (with the same number of sides) to be similar, they must satisfy two conditions:
1. Their corresponding angles must be equal.
2. The ratio of their corresponding sides must be constant (i.e., the sides must be in proportion).
The given statement claims that satisfying only the first condition (equal corresponding angles) is sufficient for two quadrilaterals to be similar. This is not true for polygons with more than three sides.
We can prove this with a counterexample.
Counterexample: Consider a square and a rectangle (which is not a square).
1. Check Corresponding Angles:
A square has four right angles, each measuring $90^\circ$.
A rectangle also has four right angles, each measuring $90^\circ$.
Therefore, all corresponding angles of a square and a rectangle are equal.
2. Check Proportionality of Corresponding Sides:
Let the square have a side length of 4 cm. Its sides are 4, 4, 4, 4.
Let the rectangle have a length of 6 cm and a width of 4 cm. Its sides are 4, 6, 4, 6.
Let's check the ratio of corresponding sides:
The ratio of one pair of corresponding sides is $\frac{4}{4} = 1$.
The ratio of the other pair of corresponding sides is $\frac{4}{6} = \frac{2}{3}$.
Since $1 \neq \frac{2}{3}$, the ratios of corresponding sides are not constant. The sides are not in proportion.
Because the second condition for similarity is not met, the square and the rectangle are not similar.
Conclusion:
No, the statement is false.
Reason: For two quadrilaterals to be similar, both conditions (equal corresponding angles and proportional corresponding sides) must be met. While triangles are a special case where angle equality implies side proportionality (AA similarity), this is not true for quadrilaterals. The counterexample of a square and a non-square rectangle shows two quadrilaterals that have equal corresponding angles but are not similar because their sides are not proportional.
Question 7. Two sides and the perimeter of one triangle are respectively three times the corresponding sides and the perimeter of the other triangle. Are the two triangles similar? Why?
Given:
Let the two triangles be $\triangle ABC$ and $\triangle DEF$.
Two sides of $\triangle ABC$ are three times the corresponding sides of $\triangle DEF$. Let's say:
$AB = 3 DE$
... (i)
$BC = 3 EF$
... (ii)
The perimeter of $\triangle ABC$ is three times the perimeter of $\triangle DEF$.
$Perimeter(\triangle ABC) = 3 \times Perimeter(\triangle DEF)$
... (iii)
To Determine:
Whether the two triangles are similar, with justification.
Solution:
Let's write out the perimeter relationship from equation (iii) in terms of the sides:
$AB + BC + AC = 3 \times (DE + EF + DF)$
$AB + BC + AC = 3 DE + 3 EF + 3 DF$
Now, we can substitute the known relationships from equations (i) and (ii) into this perimeter equation:
$(3 DE) + (3 EF) + AC = 3 DE + 3 EF + 3 DF$
We can subtract $3 DE$ and $3 EF$ from both sides of the equation, which leaves us with:
$AC = 3 DF$
So, we have found that the third pair of corresponding sides are also in the same ratio of 3:1.
Now let's check the ratios of all three pairs of corresponding sides:
From (i): $\frac{AB}{DE} = 3$
From (ii): $\frac{BC}{EF} = 3$
From our result: $\frac{AC}{DF} = 3$
Since the ratios of all three pairs of corresponding sides are equal, the triangles are similar.
$\frac{AB}{DE} = \frac{BC}{EF} = \frac{AC}{DF} = 3$
Conclusion:
Yes, the two triangles are similar.
Reason: By using the given information that two sides and the perimeter are in a 3:1 ratio, we proved that the third pair of sides must also be in a 3:1 ratio. Since all three pairs of corresponding sides of the two triangles are in the same ratio, the triangles are similar by the Side-Side-Side (SSS) similarity criterion.
Question 8. If in two right triangles, one of the acute angles of one triangle is equal to an acute angle of the other triangle, can you say that the two triangles will be similar? Why?
Given:
Two right-angled triangles.
One acute angle of the first triangle is equal to one acute angle of the second triangle.
To Determine:
Whether the two triangles are necessarily similar, with justification.
Solution:
Let the two right triangles be $\triangle ABC$ and $\triangle DEF$.
Since they are right triangles, each has one angle that measures $90^\circ$. Let's assume:
$\angle B = 90^\circ$ and $\angle E = 90^\circ$
... (i)
We are also given that one acute angle from $\triangle ABC$ (either $\angle A$ or $\angle C$) is equal to one acute angle from $\triangle DEF$ (either $\angle D$ or $\angle F$).
Let's assume the given equal acute angles are $\angle A$ and $\angle D$.
$\angle A = \angle D$
... (ii)
Now, let's compare the angles of $\triangle ABC$ and $\triangle DEF$.
From (i), we have one pair of equal angles: $\angle B = \angle E = 90^\circ$.
From (ii), we have a second pair of equal angles: $\angle A = \angle D$.
We can now apply the Angle-Angle (AA) similarity criterion. This criterion states that if two angles of one triangle are equal to two corresponding angles of another triangle, then the two triangles are similar.
Since $\triangle ABC$ and $\triangle DEF$ have two pairs of equal angles, they are similar.
Conclusion:
Yes, the two triangles will be similar.
Reason: We are given that both triangles are right triangles, so they each have a $90^\circ$ angle, which gives us one pair of equal angles. We are also given that one acute angle in the first triangle is equal to an acute angle in the second, providing a second pair of equal angles. Therefore, by the AA similarity criterion, the two triangles must be similar.
Question 9. The ratio of the corresponding altitudes of two similar triangles is $\frac{3}{5}$ . Is it correct to say that ratio of their areas is $\frac{6}{5}$ ? Why?
Given:
Two triangles are similar.
The ratio of their corresponding altitudes is $\frac{3}{5}$.
To Determine:
If the statement "the ratio of their areas is $\frac{6}{5}$" is correct, with justification.
Solution:
Let the two similar triangles be $\triangle_1$ and $\triangle_2$.
Let their corresponding altitudes be $h_1$ and $h_2$. We are given $\frac{h_1}{h_2} = \frac{3}{5}$.
We use the theorem relating the areas of similar triangles to their altitudes. The theorem states: "The ratio of the areas of two similar triangles is equal to the square of the ratio of their corresponding altitudes."
According to this theorem, the ratio of the areas is:
$\frac{Area(\triangle_1)}{Area(\triangle_2)} = \left(\frac{h_1}{h_2}\right)^2$
Now, we substitute the given ratio of the altitudes into this formula:
$\frac{Area(\triangle_1)}{Area(\triangle_2)} = \left(\frac{3}{5}\right)^2$
$\frac{Area(\triangle_1)}{Area(\triangle_2)} = \frac{3^2}{5^2} = \frac{9}{25}$
The correct ratio of the areas is $\frac{9}{25}$.
The question asks if it is correct to say the ratio of the areas is $\frac{6}{5}$.
Comparing our result with the statement: $\frac{9}{25} \neq \frac{6}{5}$.
Conclusion:
No, the statement is not correct.
Reason: The ratio of the areas of two similar triangles is equal to the square of the ratio of their corresponding altitudes, not twice the ratio. Since the ratio of the altitudes is $\frac{3}{5}$, the ratio of the areas is $(\frac{3}{5})^2 = \frac{9}{25}$. The value $\frac{6}{5}$ seems to have been obtained by incorrectly multiplying the numerator and denominator by 2 instead of squaring them.
Question 10. D is a point on side QR of ΔPQR such that PD ⊥ QR. Will it be correct to say that ΔPQD ~ ΔRPD? Why?
Given:
In $\triangle PQR$, D is a point on the side QR.
PD is perpendicular to QR ($PD \perp QR$). This means PD is an altitude of the triangle.
To Determine:
If it is correct to say that $\triangle PQD \sim \triangle RPD$, with justification.
Solution:
Let's analyze the two triangles in question: $\triangle PQD$ and $\triangle RPD$.
Since $PD \perp QR$, we know that the angles at D are right angles.
$\angle PDQ = 90^\circ$ (in $\triangle PQD$)
$\angle PDR = 90^\circ$ (in $\triangle RPD$)
So, we have one pair of equal angles: $\angle PDQ = \angle PDR$.
For the two triangles to be similar, we would need to satisfy one of the similarity criteria (AA, SAS, or SSS). Since we have one pair of equal angles, let's consider the AA and SAS criteria.
AA Similarity: To use this criterion, we would need another pair of corresponding angles to be equal. The correspondence in $\triangle PQD \sim \triangle RPD$ would be P $\leftrightarrow$ R, Q $\leftrightarrow$ P, and D $\leftrightarrow$ D. This means we would need $\angle Q = \angle RPD$ and $\angle QPD = \angle R$. This condition is not given and is not generally true for any triangle with an altitude.
SAS Similarity: To use this criterion, the sides including the equal angles must be in proportion. The sides including the right angles are PD, QD in $\triangle PQD$ and PD, RD in $\triangle RPD$. We would need $\frac{PD}{RD} = \frac{QD}{PD}$. This would mean $PD^2 = QD \cdot RD$. This is only true in a special case where the main triangle $\triangle PQR$ is a right-angled triangle with the right angle at P (this is the Geometric Mean Theorem).
Since the problem does not state that $\triangle PQR$ is a right triangle or provide any other information about its angles or sides, we cannot assume that any of these extra conditions are met.
Conclusion:
No, it is not correct to say that $\triangle PQD \sim \triangle RPD$ based only on the given information.
Reason: The fact that PD is an altitude only provides one pair of equal angles ($\angle PDQ = \angle PDR = 90^\circ$). This is not sufficient to prove similarity. The triangles would only be similar in special cases (e.g., if $\triangle PQR$ were a right-angled triangle at P). For a general triangle, these two smaller triangles formed by the altitude are not similar to each other.
Question 11. In Fig. 6.5, if ∠D =∠C, then is it true that ΔADE ~ ΔACB? Why?
Answer:
Given:
In the figure, we have a triangle $\triangle ABC$ and a line segment DE intersecting sides AB and AC at points D and E respectively.
The angles marked as equal are $\angle ADE$ and $\angle ACB$.
So, $\angle ADE = \angle ACB$.
To Determine:
Whether the similarity statement $\triangle ADE \sim \triangle ACB$ is true, and provide the reason.
Solution:
To determine if the triangles are similar, we can check if they satisfy the Angle-Angle (AA) similarity criterion. This criterion states that if two angles of one triangle are equal to two corresponding angles of another triangle, then the two triangles are similar.
Let's compare the angles of the small triangle, $\triangle ADE$, with the angles of the large triangle, $\triangle ACB$.
1. We are given one pair of equal angles:
$\angle ADE = \angle ACB$
(Given)
2. We can observe from the figure that the angle at vertex A, which is $\angle DAE$ for the small triangle and $\angle CAB$ for the large triangle, is the same angle.
$\angle DAE = \angle CAB$
[Common angle]
Since we have found two pairs of corresponding angles that are equal, the conditions for the AA similarity criterion are met.
Therefore, the triangles are similar.
Now, we must check if the vertex correspondence in the statement $\triangle ADE \sim \triangle ACB$ is correct.
The correspondence is determined by the equal angles:
The angle at vertex A in $\triangle ADE$ corresponds to the angle at vertex A in $\triangle ACB$.
The angle at vertex D in $\triangle ADE$ corresponds to the angle at vertex C in $\triangle ACB$.
By implication, the remaining angle at vertex E in $\triangle ADE$ must correspond to the remaining angle at vertex B in $\triangle ACB$.
So, the correct similarity statement is indeed $\triangle ADE \sim \triangle ACB$.
Conclusion:
Yes, the statement is true.
Reason: In triangles $\triangle ADE$ and $\triangle ACB$, we have $\angle ADE = \angle ACB$ (given) and $\angle A$ is common to both triangles. Since two pairs of corresponding angles are equal, the triangles are similar by the AA similarity criterion with the correspondence A $\leftrightarrow$ A, D $\leftrightarrow$ C, and E $\leftrightarrow$ B.
Question 12. Is it true to say that if in two triangles, an angle of one triangle is equal to an angle of another triangle and two sides of one triangle are proportional to the two sides of the other triangle, then the triangles are similar? Give reasons for your answer
Answer:
Given Statement:
"If in two triangles, an angle of one triangle is equal to an angle of another triangle and two sides of one triangle are proportional to the two sides of the other triangle, then the triangles are similar."
To Determine:
Whether the given statement is true, with justification.
Solution:
The statement as worded is false. It is a misstatement of the Side-Angle-Side (SAS) similarity criterion.
The correct SAS similarity criterion states: "If an angle of one triangle is equal to an angle of another triangle and the sides including these angles are in proportion, then the two triangles are similar."
The crucial part missing from the given statement is that the equal angle must be the angle included between the two proportional sides. If the equal angle is not the included angle, the triangles are not necessarily similar.
We can prove this with a counterexample.
Counterexample:
Consider two triangles, $\triangle ABC$ and $\triangle DEF$.
Let's construct $\triangle ABC$ such that:
- $AB = 4$ cm
- $AC = 6$ cm
- $\angle A = 40^\circ$ (This is the angle included between sides AB and AC)
Now, let's construct $\triangle DEF$ to satisfy the conditions of the given statement but fail the SAS criterion:
- Let $DE = 8$ cm (proportional to AB, ratio is 2)
- Let $DF = 12$ cm (proportional to AC, ratio is 2)
- Let $\angle E = 40^\circ$ (equal to an angle in $\triangle ABC$, but it is *not* the included angle)
Now, let's check if this setup satisfies the conditions of the given statement:
1. Is an angle of one triangle equal to an angle of another? Yes, $\angle A = \angle E = 40^\circ$.
2. Are two sides of one triangle proportional to two sides of the other? Yes, $\frac{AB}{DE} = \frac{4}{8} = \frac{1}{2}$ and $\frac{AC}{DF} = \frac{6}{12} = \frac{1}{2}$. The sides are proportional.
So, our two triangles satisfy the conditions of the statement.
Now, are the triangles similar?
For the triangles to be similar by SAS, the included angles must be equal. In $\triangle ABC$, the included angle between sides AB and AC is $\angle A = 40^\circ$. In $\triangle DEF$, the included angle between sides DE and DF is $\angle D$.
We do not know the value of $\angle D$, but we know $\angle E = 40^\circ$. Unless $\triangle DEF$ is an isosceles triangle with $\angle D = \angle E = 40^\circ$ (which is not guaranteed), $\angle D$ will not be equal to $\angle A$. Therefore, the triangles are not similar by the SAS criterion.
Conclusion:
No, the statement is false.
Reason: The statement is missing the critical condition that the equal angle must be the one included between the proportional sides. Without this condition, the triangles are not guaranteed to be similar, as demonstrated by the counterexample.
Sample Question 1 to 3 (Before Exercise 6.3)
Sample Question 1: Legs (sides other than the hypotenuse) of a right triangle are of lengths 16cm and 8 cm. Find the length of the side of the largest square that can be inscribed in the triangle.
Answer:
Given:
The legs (sides other than the hypotenuse) of a right triangle have lengths:
$a = 16$ cm
$b = 8$ cm
To Find:
The length of the side of the largest square that can be inscribed in the triangle.
Solution:
There are two primary ways a square can be inscribed in a right-angled triangle. We will calculate the side length for each case and then compare them to find the largest one.
Case 1: One vertex of the square coincides with the right-angle vertex of the triangle.
Let the side length of the square in this case be $s_1$.
The formula for the side length is given by:
$s_1 = \frac{a \times b}{a+b}$
Substituting the given values $a = 16$ and $b = 8$:
$s_1 = \frac{16 \times 8}{16 + 8} = \frac{128}{24}$
Simplifying the fraction:
$s_1 = \frac{\cancel{128}^{16}}{\cancel{24}_{3}} = \frac{16}{3}$ cm
... (i)
So, $s_1 \approx 5.33$ cm.
Case 2: One side of the square lies on the hypotenuse of the triangle.
Let the side length of the square in this case be $s_2$.
First, we need to find the length of the hypotenuse, $c$, using the Pythagorean theorem, and the altitude, $h$, from the right angle to the hypotenuse.
Hypotenuse (c):
$c = \sqrt{a^2 + b^2} = \sqrt{16^2 + 8^2} = \sqrt{256 + 64} = \sqrt{320}$
$c = \sqrt{64 \times 5} = 8\sqrt{5}$ cm
Altitude to the hypotenuse (h):
$h = \frac{a \times b}{c} = \frac{16 \times 8}{8\sqrt{5}} = \frac{16}{\sqrt{5}}$ cm
The formula for the side length $s_2$ is given by:
$s_2 = \frac{c \times h}{c+h}$
Substituting the values of $c$ and $h$:
$s_2 = \frac{8\sqrt{5} \times \frac{16}{\sqrt{5}}}{8\sqrt{5} + \frac{16}{\sqrt{5}}} = \frac{128}{\frac{8\sqrt{5}(\sqrt{5}) + 16}{\sqrt{5}}} = \frac{128}{\frac{8(5) + 16}{\sqrt{5}}}$
$s_2 = \frac{128}{\frac{40 + 16}{\sqrt{5}}} = \frac{128}{\frac{56}{\sqrt{5}}} = \frac{128\sqrt{5}}{56}$
Simplifying the fraction:
$s_2 = \frac{\cancel{128}^{16}\sqrt{5}}{\cancel{56}_{7}} = \frac{16\sqrt{5}}{7}$ cm
... (ii)
Since $\sqrt{5} \approx 2.236$, we have $s_2 \approx \frac{16 \times 2.236}{7} \approx \frac{35.776}{7} \approx 5.11$ cm.
Comparison:
Now, we compare the side lengths from both cases to find the largest possible square.
From (i), $s_1 = \frac{16}{3} \approx 5.33$ cm.
From (ii), $s_2 = \frac{16\sqrt{5}}{7} \approx 5.11$ cm.
Clearly, $s_1 > s_2$.
Conclusion:
The largest square that can be inscribed in the given right triangle has a side length corresponding to Case 1.
Therefore, the length of the side of the largest square is $\frac{16}{3}$ cm.
Sample Question 2: Hypotenuse of a right triangle is 25 cm and out of the remaining two sides, one is longer than the other by 5 cm. Find the lengths of the other two sides.
Answer:
Given:
For a right-angled triangle:
Length of the hypotenuse = $25$ cm.
One of the other two sides (legs) is longer than the other by $5$ cm.
To Find:
The lengths of the two legs of the right triangle.
Solution:
Let the length of the shorter leg be $x$ cm.
According to the given condition, the length of the longer leg is $(x + 5)$ cm.
We can use the Pythagorean theorem for a right-angled triangle, which states:
$(\text{Base})^2 + (\text{Perpendicular})^2 = (\text{Hypotenuse})^2$
Substituting the values into the theorem:
$x^2 + (x+5)^2 = 25^2$
[By Pythagorean Theorem] ... (i)
Now, we solve this equation for $x$.
Expanding the term $(x+5)^2$ using the identity $(a+b)^2 = a^2 + 2ab + b^2$:
$x^2 + (x^2 + 2 \cdot x \cdot 5 + 5^2) = 625$
$x^2 + x^2 + 10x + 25 = 625$
Combine like terms:
$2x^2 + 10x + 25 = 625$
To form a standard quadratic equation ($ax^2 + bx + c = 0$), subtract $625$ from both sides:
$2x^2 + 10x + 25 - 625 = 0$
$2x^2 + 10x - 600 = 0$
To simplify the equation, we can divide the entire equation by $2$:
$x^2 + 5x - 300 = 0$
... (ii)
We can solve this quadratic equation by factoring. We need to find two numbers that multiply to $-300$ and add to $+5$. These numbers are $+20$ and $-15$.
$x^2 + 20x - 15x - 300 = 0$
$x(x+20) - 15(x+20) = 0$
$(x-15)(x+20) = 0$
This gives two possible values for $x$:
$x - 15 = 0 \implies x = 15$
$x + 20 = 0 \implies x = -20$
Since $x$ represents the length of a side of a triangle, it cannot be negative. Therefore, we discard the value $x = -20$.
The only valid solution is $x = 15$.
Now we find the lengths of the two legs:
Shorter leg = $x = 15$ cm.
Longer leg = $x + 5 = 15 + 5 = 20$ cm.
Verification:
Let's check if these lengths satisfy the Pythagorean theorem:
$15^2 + 20^2 = 225 + 400 = 625$
And the hypotenuse squared is $25^2 = 625$.
Since $625 = 625$, our calculated side lengths are correct.
Conclusion:
The lengths of the other two sides of the right triangle are 15 cm and 20 cm.
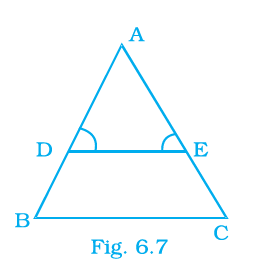
Sample Question 3: In Fig 6.7,
∠D =∠E and $\frac{AD}{DB}$ = $\frac{AE}{EC}$ . Prove that BAC is an isosceles triangle.
Answer:
Given:
In the given figure, we have a triangle ABC with a line segment DE intersecting sides AB and AC at points D and E respectively, such that:
$\angle ADE = \angle AED$
... (i)
$\frac{AD}{DB} = \frac{AE}{EC}$
... (ii)
To Prove:
Triangle BAC is an isosceles triangle.
Proof:
From the given condition (ii):
$\frac{AD}{DB} = \frac{AE}{EC}$
(Given)
According to the Converse of the Basic Proportionality Theorem (also known as Thales' Theorem), if a line divides any two sides of a triangle in the same ratio, then the line must be parallel to the third side.
Therefore, we can conclude that DE is parallel to BC.
DE || BC
... (iii)
Now, since DE || BC and AB is a transversal line that intersects them, the corresponding angles are equal.
$\angle ADE = \angle ABC$
(Corresponding angles) ... (iv)
Similarly, since DE || BC and AC is a transversal line that intersects them, the corresponding angles are equal.
$\angle AED = \angle ACB$
(Corresponding angles) ... (v)
We are also given that:
$\angle ADE = \angle AED$
(Given from (i))
From equations (iv) and (v), by substituting the given condition, we get:
$\angle ABC = \angle ACB$
In $\triangle$ABC, since two angles ($\angle B$ and $\angle C$) are equal, the sides opposite to these equal angles must also be equal.
AC = AB
(Sides opposite to equal angles)
A triangle with two equal sides is defined as an isosceles triangle.
Therefore, $\triangle$BAC is an isosceles triangle.
Hence, Proved.
Alternate Solution
Proof:
We are given that in $\triangle$ADE:
$\angle ADE = \angle AED$
(Given)
In a triangle, sides opposite to equal angles are equal in length. Thus, in $\triangle$ADE:
AD = AE
(Sides opposite to equal angles) ... (a)
We are also given the ratio:
$\frac{AD}{DB} = \frac{AE}{EC}$
(Given) ... (b)
Substitute the value of AE from equation (a) into equation (b):
$\frac{AD}{DB} = \frac{AD}{EC}$
Since AD represents a length, $AD \neq 0$. We can cancel AD from both sides of the equation.
$\frac{1}{DB} = \frac{1}{EC}$
Taking the reciprocal on both sides, we get:
DB = EC
... (c)
Now, let's consider the sides AB and AC of the larger triangle $\triangle$ABC.
From the figure, we can write:
$AB = AD + DB$
$AC = AE + EC$
Adding equations (a) and (c):
$AD + DB = AE + EC$
This directly implies:
AB = AC
Since two sides of $\triangle$BAC are equal, it is an isosceles triangle.
Hence, Proved.
Exercise 6.3
Question 1. In a ΔPQR, PR2 – PQ2 = QR2 and M is a point on side PR such that QM ⊥ PR.
Prove that QM2 = PM × MR.
Answer:
Given:
In a $\triangle$PQR, we are given that:
PR2 – PQ2 = QR2
... (i)
Also, M is a point on the side PR such that QM is perpendicular to PR.
QM $\perp$ PR
... (ii)
To Prove:
QM2 = PM × MR
Proof:
From the given relation (i):
$PR^2 – PQ^2 = QR^2$
Rearranging the terms, we get:
$PR^2 = PQ^2 + QR^2$
This equation is in the form of the Pythagorean theorem. By the converse of the Pythagorean theorem, if the square of one side of a triangle is equal to the sum of the squares of the other two sides, then the angle opposite the first side is a right angle.
Here, the side PR is the hypotenuse. Therefore, the angle opposite to PR, which is $\angle$PQR, must be $90^\circ$.
So, $\triangle$PQR is a right-angled triangle, with the right angle at Q.
Now, consider the triangles $\triangle$QMR and $\triangle$PMQ.
We are given that QM $\perp$ PR, which means:
$\angle QMP = \angle QMR = 90^\circ$
In the right-angled $\triangle$PQR, let's assume $\angle R = \theta$.
Then, since the sum of angles in a triangle is $180^\circ$:
$\angle P = 180^\circ - 90^\circ - \theta = 90^\circ - \theta$.
Now, let's analyze the smaller triangles:
In $\triangle$QMR:
$\angle QMR = 90^\circ$
(Given)
$\angle MRQ = \angle R = \theta$
Therefore, $\angle MQR = 180^\circ - 90^\circ - \theta = 90^\circ - \theta$.
In $\triangle$PMQ:
$\angle QMP = 90^\circ$
(Given)
$\angle MPQ = \angle P = 90^\circ - \theta$
Therefore, $\angle PQM = 180^\circ - 90^\circ - (90^\circ - \theta) = \theta$.
Now, we compare the angles of $\triangle$QMR and $\triangle$PMQ:
$\angle MRQ = \theta$ and $\angle PQM = \theta \implies \angle MRQ = \angle PQM$.
$\angle MQR = 90^\circ - \theta$ and $\angle MPQ = 90^\circ - \theta \implies \angle MQR = \angle MPQ$.
$\angle QMR = 90^\circ$ and $\angle QMP = 90^\circ \implies \angle QMR = \angle QMP$.
Since all corresponding angles are equal, the two triangles are similar by the AAA (Angle-Angle-Angle) similarity criterion.
$\triangle$QMR $\sim$ $\triangle$PMQ
(By AAA similarity)
When two triangles are similar, the ratio of their corresponding sides is equal. Therefore:
$\frac{QM}{PM} = \frac{MR}{MQ} = \frac{QR}{PQ}$
Taking the first two parts of the ratio:
$\frac{QM}{PM} = \frac{MR}{MQ}$
Cross-multiplying the terms, we get:
$QM \times MQ = PM \times MR$
$QM^2 = PM \times MR$
Hence, Proved.
Question 2. Find the value of x for which DE || AB in Fig. 6.8.
Answer:
Given:
In $\triangle CAB$, points D and E are on sides CA and CB respectively.
The lengths of the segments are:
$CD = (x+3)$ cm
$DA = (3x+19)$ cm
$CE = x$ cm
$EB = (3x+4)$ cm
To Find:
The value of x for which $DE || AB$.
Solution:
For $DE$ to be parallel to $AB$ in $\triangle CAB$, the Basic Proportionality Theorem (BPT) must hold.
According to the converse of the BPT, if a line divides any two sides of a triangle proportionally, then it is parallel to the third side.
Therefore, for $DE || AB$, we must have:
$\frac{CD}{DA} = \frac{CE}{EB}$
Substitute the given expressions for the segment lengths:
$\frac{x+3}{3x+19} = \frac{x}{3x+4}$
Cross-multiply the equation:
$(x+3)(3x+4) = x(3x+19)$
Expand both sides:
$x(3x) + x(4) + 3(3x) + 3(4) = x(3x) + x(19)$
$3x^2 + 4x + 9x + 12 = 3x^2 + 19x$
Combine like terms on the left side:
$3x^2 + 13x + 12 = 3x^2 + 19x$
Subtract $3x^2$ from both sides:
$13x + 12 = 19x$
Subtract $13x$ from both sides:
$12 = 19x - 13x$
$12 = 6x$
Divide by 6:
$x = \frac{12}{6}$
$x = 2$
We should verify that this value of x results in positive lengths for all segments:
$CD = 2+3 = 5 > 0$
$DA = 3(2)+19 = 6+19 = 25 > 0$
$CE = 2 > 0$
$EB = 3(2)+4 = 6+4 = 10 > 0$
Since all lengths are positive, the value $x=2$ is valid.
Thus, for $DE || AB$, the value of x is 2.
Question 3. In Fig. 6.9, if ∠1 =∠2 and ΔNSQ ≅ ΔMTR, then prove that ΔPTS ~ ΔPRQ.
Answer:
Given:
In the given figure, we have:
$\triangle NSQ \cong \triangle MTR$
$\angle 1 = \angle 2$
To prove:
$\triangle PTS \sim \triangle PRQ$
Proof:
Since, $\triangle NSQ \cong \triangle MTR$ (Given), their corresponding parts are equal.
$SQ = TR$
[By CPCTC] ... (i)
Also, we are given that $\angle 1 = \angle 2$.
In $\triangle$PTS, this means $\angle PST = \angle PTS$.
$PT = PS$
[Sides opposite to equal angles are equal] ... (ii)
From equations (i) and (ii), we can write the ratio:
$\frac{PS}{SQ} = \frac{PT}{TR}$
By the converse of the Basic Proportionality Theorem, since the line segment ST divides the sides PQ and PR in the same ratio, ST must be parallel to the third side QR.
$ST \parallel QR$
(By Converse of B.P.T.)
Now, since $ST \parallel QR$ and PQ is the transversal, the corresponding angles are equal.
$\angle 1 = \angle PQR$
(Corresponding angles)
Similarly, since $ST \parallel QR$ and PR is the transversal, the corresponding angles are equal.
$\angle 2 = \angle PRQ$
(Corresponding angles)
Now, let's compare $\triangle PTS$ and $\triangle PRQ$.
$\angle P = \angle P$
(Common angle)
$\angle 1 = \angle PQR$
(Proved above)
$\angle 2 = \angle PRQ$
(Proved above)
Since all three corresponding angles of the triangles are equal, by the AAA (Angle-Angle-Angle) similarity criterion, the triangles are similar.
$\therefore \triangle PTS \sim \triangle PRQ$
Hence, Proved.
Question 4. Diagonals of a trapezium PQRS intersect each other at the point O, PQ || RS and PQ = 3 RS. Find the ratio of the areas of triangles POQ and ROS.
Answer:
Given:
PQRS is a trapezium in which PQ is parallel to RS (PQ || RS).
The diagonals PR and QS intersect each other at the point O.
The length of side PQ is three times the length of side RS, i.e., $PQ = 3 RS$.
To Find:
The ratio of the areas of $\triangle POQ$ and $\triangle ROS$.
That is, $\frac{\text{ar}(\triangle POQ)}{\text{ar}(\triangle ROS)}$.
Solution:
We need to find the ratio of the areas of $\triangle POQ$ and $\triangle ROS$. To do this, we will first prove that these two triangles are similar.
Consider the triangles $\triangle POQ$ and $\triangle ROS$.
Since PQ || RS and PR is a transversal line intersecting them, the alternate interior angles are equal.
$\angle OPQ = \angle ORS$
(Alternate interior angles)
Similarly, since PQ || RS and QS is a transversal line intersecting them, the alternate interior angles are equal.
$\angle OQP = \angle OSR$
(Alternate interior angles)
Also, the angles at the intersection of the diagonals are vertically opposite angles, which are always equal.
$\angle POQ = \angle ROS$
(Vertically opposite angles)
Since all three corresponding angles of $\triangle POQ$ and $\triangle ROS$ are equal, the two triangles are similar by the AAA (Angle-Angle-Angle) similarity criterion.
$\triangle POQ \sim \triangle ROS$
(By AAA similarity)
Now, we know that the ratio of the areas of two similar triangles is equal to the square of the ratio of their corresponding sides.
$\frac{\text{ar}(\triangle POQ)}{\text{ar}(\triangle ROS)} = \left(\frac{PQ}{RS}\right)^2 = \left(\frac{OQ}{OS}\right)^2 = \left(\frac{PO}{RO}\right)^2$
... (i)
We are given that $PQ = 3 RS$. We can substitute this into equation (i).
$\frac{\text{ar}(\triangle POQ)}{\text{ar}(\triangle ROS)} = \left(\frac{3 RS}{RS}\right)^2$
Canceling RS from the numerator and denominator:
$\frac{\text{ar}(\triangle POQ)}{\text{ar}(\triangle ROS)} = \left(\frac{3}{1}\right)^2$
$\frac{\text{ar}(\triangle POQ)}{\text{ar}(\triangle ROS)} = \frac{9}{1}$
Therefore, the ratio of the areas of $\triangle POQ$ and $\triangle ROS$ is 9 : 1.
Final Answer:
The ratio of the areas of triangles POQ and ROS is 9 : 1.
Question 5. In Fig. 6.10, if AB || DC and AC and PQ intersect each other at the point O, prove that OA . CQ = OC . AP
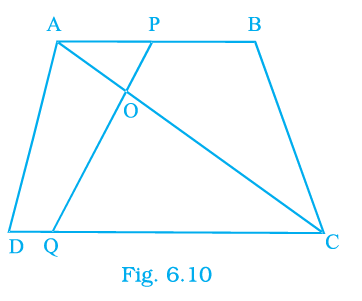
Answer:
Given:
In the given figure, $AB || DC$.
AC and PQ intersect each other at the point O.
P is a point on AB and Q is a point on DC.
To Prove:
$OA \cdot CQ = OC \cdot AP$.
Proof:
Consider $\triangle PAO$ and $\triangle QCO$.
Since $AB || DC$, and AC is a transversal, the alternate interior angles are equal.
$\angle PAO = \angle QCO$
$\angle OAP = \angle OCQ$
(Alternate interior angles, since $AB || DC$)
The lines AC and PQ intersect at O. The angles opposite to each other at the intersection are vertically opposite angles, which are equal.
$\angle AOP = \angle COQ$
$\angle AOP = \angle COQ$
(Vertically opposite angles)
Now, in $\triangle PAO$ and $\triangle QCO$, we have two pairs of corresponding angles that are equal ($\angle OAP = \angle OCQ$ and $\angle AOP = \angle COQ$).
Therefore, by AA similarity criterion, $\triangle PAO \sim \triangle QCO$.
When two triangles are similar, the ratio of their corresponding sides is equal.
Thus, we have:
$\frac{OA}{OC} = \frac{AP}{CQ} = \frac{PO}{QO}$
Taking the first two ratios:
$\frac{OA}{OC} = \frac{AP}{CQ}$
Cross-multiplying the terms, we get:
$OA \cdot CQ = OC \cdot AP$
This is the required equation to prove.
Hence Proved.
Question 6. Find the altitude of an equilateral triangle of side 8 cm.
Answer:
Given:
An equilateral triangle with a side length of 8 cm.
To Find:
The length of the altitude of the equilateral triangle.
Solution:
Let $\triangle ABC$ be an equilateral triangle with side length $a = 8$ cm. So, $AB = BC = CA = 8$ cm.
Let AD be the altitude drawn from vertex A to the base BC.
In an equilateral triangle, the altitude to a side also bisects that side. Therefore, point D is the midpoint of BC.
$BD = DC = \frac{1}{2} BC = \frac{1}{2} \times 8 = 4$ cm
Since AD is an altitude, it is perpendicular to BC. Thus, $\triangle ADB$ is a right-angled triangle with $\angle ADB = 90^\circ$.
By applying the Pythagorean theorem to $\triangle ADB$:
$AB^2 = AD^2 + BD^2$
Substitute the known values:
$8^2 = AD^2 + 4^2$
$64 = AD^2 + 16$
Rearranging the equation to solve for $AD^2$:
$AD^2 = 64 - 16 = 48$
Taking the square root of both sides:
$AD = \sqrt{48} = \sqrt{16 \times 3} = 4\sqrt{3}$ cm
Thus, the altitude of the equilateral triangle is $4\sqrt{3}$ cm.
Alternate Solution:
We can use the direct formula for the altitude ($h$) of an equilateral triangle with side length $a$.
$h = \frac{\sqrt{3}}{2} a$
Given the side length $a = 8$ cm, we substitute this value into the formula:
$h = \frac{\sqrt{3}}{2} \times 8$
$h = \sqrt{3} \times \frac{\cancel{8}^4}{\cancel{2}_1} = 4\sqrt{3}$ cm
Final Answer:
The altitude of the equilateral triangle is $4\sqrt{3}$ cm.
Question 7. If ΔABC ~ ΔDEF, AB = 4 cm, DE = 6 cm, EF = 9 cm and FD = 12 cm, find the perimeter of ABC.
Answer:
Given:
Triangle ABC is similar to triangle DEF ($\triangle ABC \sim \triangle DEF$).
The lengths of the sides are:
$AB = 4$ cm
$DE = 6$ cm
$EF = 9$ cm
$FD = 12$ cm
To Find:
The perimeter of $\triangle ABC$.
Solution:
Since $\triangle ABC \sim \triangle DEF$, the ratio of their corresponding sides is equal.
$\frac{AB}{DE} = \frac{BC}{EF} = \frac{AC}{DF}$
... (i)
Substitute the given values into this proportion:
$\frac{4}{6} = \frac{BC}{9} = \frac{AC}{12}$
The ratio of the sides is $\frac{4}{6}$, which simplifies to $\frac{2}{3}$.
Now, we can find the lengths of the unknown sides BC and AC.
To find BC:
$\frac{2}{3} = \frac{BC}{9}$
$BC = \frac{2}{3} \times 9 = 2 \times 3 = 6$ cm
To find AC:
$\frac{2}{3} = \frac{AC}{12}$
$AC = \frac{2}{3} \times 12 = 2 \times 4 = 8$ cm
The sides of $\triangle ABC$ are $AB = 4$ cm, $BC = 6$ cm, and $AC = 8$ cm.
The perimeter of a triangle is the sum of the lengths of its sides.
Perimeter of $\triangle ABC = AB + BC + AC$
$Perimeter = 4 + 6 + 8 = 18$ cm
Alternate Solution:
The ratio of the perimeters of two similar triangles is equal to the ratio of their corresponding sides.
$\frac{\text{Perimeter}(\triangle ABC)}{\text{Perimeter}(\triangle DEF)} = \frac{AB}{DE}$
First, calculate the perimeter of $\triangle DEF$.
Perimeter of $\triangle DEF = DE + EF + FD$
$Perimeter(\triangle DEF) = 6 + 9 + 12 = 27$ cm
Now, substitute the known values into the ratio formula:
$\frac{\text{Perimeter}(\triangle ABC)}{27} = \frac{4}{6}$
Simplify the ratio $\frac{4}{6}$ to $\frac{2}{3}$:
$\frac{\text{Perimeter}(\triangle ABC)}{27} = \frac{2}{3}$
Solve for the perimeter of $\triangle ABC$:
$\text{Perimeter}(\triangle ABC) = \frac{2}{3} \times 27 = 2 \times 9 = 18$ cm
Final Answer:
The perimeter of triangle ABC is 18 cm.
Question 8. In Fig. 6.11, if DE || BC, find the ratio of ar (ADE) and ar (DECB).
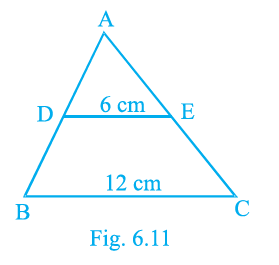
Answer:
Given:
In the given figure, we have a triangle ABC and a line segment DE.
DE is parallel to BC (DE || BC).
The lengths of the parallel sides are:
DE = 6 cm
BC = 12 cm
To Find:
The ratio of the area of $\triangle ADE$ to the area of the trapezium DECB.
That is, $\frac{\text{ar}(\triangle ADE)}{\text{ar}(DECB)}$.
Solution:
First, we need to establish the relationship between $\triangle ADE$ and $\triangle ABC$.
In $\triangle ADE$ and $\triangle ABC$:
Since DE || BC and AB is a transversal line, the corresponding angles are equal.
$\angle ADE = \angle ABC$
(Corresponding angles)
Similarly, since DE || BC and AC is a transversal line, the corresponding angles are equal.
$\angle AED = \angle ACB$
(Corresponding angles)
The angle at vertex A is common to both triangles.
$\angle DAE = \angle BAC$
(Common angle)
Since the corresponding angles are equal, the two triangles are similar by the AA (or AAA) similarity criterion.
$\triangle ADE \sim \triangle ABC$
(By AA similarity)
Now, we use the theorem that states that the ratio of the areas of two similar triangles is equal to the square of the ratio of their corresponding sides.
$\frac{\text{ar}(\triangle ADE)}{\text{ar}(\triangle ABC)} = \left(\frac{DE}{BC}\right)^2$
... (i)
Substitute the given values of DE and BC into the equation:
$\frac{\text{ar}(\triangle ADE)}{\text{ar}(\triangle ABC)} = \left(\frac{6}{12}\right)^2 = \left(\frac{1}{2}\right)^2 = \frac{1}{4}$
This means that $\text{ar}(\triangle ABC) = 4 \times \text{ar}(\triangle ADE)$.
From the figure, the area of the trapezium DECB can be calculated by subtracting the area of the smaller triangle from the area of the larger triangle.
ar(DECB) = ar($\triangle$ABC) - ar($\triangle$ADE)
Now, substitute ar($\triangle$ABC) with $4 \times$ ar($\triangle$ADE):
ar(DECB) = $4 \times$ ar($\triangle$ADE) - ar($\triangle$ADE)
ar(DECB) = $3 \times$ ar($\triangle$ADE)
Now we can find the required ratio:
$\frac{\text{ar}(\triangle ADE)}{\text{ar}(DECB)} = \frac{\text{ar}(\triangle ADE)}{3 \times \text{ar}(\triangle ADE)}$
Canceling ar($\triangle$ADE) from the numerator and the denominator, we get:
$\frac{\text{ar}(\triangle ADE)}{\text{ar}(DECB)} = \frac{1}{3}$
The ratio of ar(ADE) to ar(DECB) is 1:3.
Final Answer:
The required ratio of ar (ADE) and ar (DECB) is 1 : 3.
Question 9. ABCD is a trapezium in which AB || DC and P and Q are points on AD and BC, respectively such that PQ || DC. If PD = 18 cm, BQ = 35 cm and QC = 15 cm, find AD.
Answer:
Given:
ABCD is a trapezium with $AB \parallel DC$.
P is a point on AD and Q is a point on BC such that $PQ \parallel DC$.
The lengths of the segments are:
$PD = 18$ cm
$BQ = 35$ cm
$QC = 15$ cm
To Find:
The length of the side AD.
Solution:
We are given that in trapezium ABCD, $AB \parallel DC$.
We are also given that $PQ \parallel DC$.
Since lines parallel to the same line are parallel to each other, we have $AB \parallel PQ \parallel DC$.
According to a property of trapeziums, a line drawn parallel to the parallel sides intersects the non-parallel sides in a proportional manner. This is a result derived from the Basic Proportionality Theorem.
Therefore, for the non-parallel sides AD and BC, we have the following ratio:
$\frac{AP}{PD} = \frac{BQ}{QC}$
... (i)
Substitute the given values into this equation:
$\frac{AP}{18} = \frac{35}{15}$
Simplify the fraction on the right side:
$\frac{AP}{18} = \frac{\cancel{35}^7}{\cancel{15}_3} = \frac{7}{3}$
Now, solve for AP by multiplying both sides by 18:
$AP = \frac{7}{3} \times 18 = 7 \times 6 = 42$ cm
The total length of the side AD is the sum of the lengths of the segments AP and PD.
$AD = AP + PD$
Substitute the calculated value of AP and the given value of PD:
$AD = 42 + 18 = 60$ cm
Final Answer:
The length of AD is 60 cm.
Question 10. Corresponding sides of two similar triangles are in the ratio of 2 : 3. If the area of the smaller triangle is 48 cm2 , find the area of the larger triangle.
Answer:
Given:
Two triangles are similar.
The ratio of their corresponding sides is $2 : 3$.
The area of the smaller triangle is $48 \text{ cm}^2$.
To Find:
The area of the larger triangle.
Solution:
Let the two similar triangles be $\triangle_{small}$ and $\triangle_{large}$.
Let the corresponding sides be $s_{small}$ and $s_{large}$.
We are given the ratio of the sides:
$\frac{s_{small}}{s_{large}} = \frac{2}{3}$
We are also given the area of the smaller triangle:
$\text{ar}(\triangle_{small}) = 48 \text{ cm}^2$.
According to the theorem on the areas of similar triangles, the ratio of the areas of two similar triangles is equal to the square of the ratio of their corresponding sides.
$\frac{\text{ar}(\triangle_{small})}{\text{ar}(\triangle_{large})} = \left(\frac{s_{small}}{s_{large}}\right)^2$
... (i)
Substitute the given values into this equation:
$\frac{48}{\text{ar}(\triangle_{large})} = \left(\frac{2}{3}\right)^2$
Calculate the square of the ratio:
$\frac{48}{\text{ar}(\triangle_{large})} = \frac{4}{9}$
Now, we solve for the area of the larger triangle by cross-multiplication:
$4 \times \text{ar}(\triangle_{large}) = 48 \times 9$
$\text{ar}(\triangle_{large}) = \frac{48 \times 9}{4}$
$\text{ar}(\triangle_{large}) = 12 \times 9 = 108$
So, the area of the larger triangle is $108 \text{ cm}^2$.
Final Answer:
The area of the larger triangle is $108 \text{ cm}^2$.
Question 11. In a triangle PQR, N is a point on PR such that QN ⊥ PR . If PN. NR = QN2 , prove that∠PQR = 90° .
Answer:
Given:
In $\triangle PQR$, N is a point on side PR such that $QN \perp PR$.
Also, the lengths of the segments are related by the equation: $PN \cdot NR = QN^2$.
To Prove:
$\angle PQR = 90^\circ$.
Proof:
Since $QN \perp PR$, it means that $\angle QNP = 90^\circ$ and $\angle QNR = 90^\circ$.
This implies that $\triangle QNP$ and $\triangle QNR$ are right-angled triangles.
In the right-angled triangle $\triangle QNP$, by the Pythagorean theorem:
$PQ^2 = PN^2 + QN^2$
... (i)
In the right-angled triangle $\triangle QNR$, by the Pythagorean theorem:
$QR^2 = NR^2 + QN^2$
... (ii)
Adding equations (i) and (ii):
$PQ^2 + QR^2 = (PN^2 + QN^2) + (NR^2 + QN^2)$
$PQ^2 + QR^2 = PN^2 + NR^2 + 2QN^2$
... (iii)
We are given the relation $PN \cdot NR = QN^2$.
Substitute this into equation (iii):
$PQ^2 + QR^2 = PN^2 + NR^2 + 2(PN \cdot NR)$
The right side of this equation is in the form of the algebraic identity $(a+b)^2 = a^2 + b^2 + 2ab$.
Therefore, $PN^2 + NR^2 + 2(PN \cdot NR) = (PN + NR)^2$.
Since N is a point on the line segment PR, we have $PR = PN + NR$.
So, the equation becomes:
$PQ^2 + QR^2 = (PN + NR)^2 = PR^2$
This final relation, $PQ^2 + QR^2 = PR^2$, is the statement of the Pythagorean theorem for $\triangle PQR$.
By the converse of the Pythagorean theorem, if the square of one side of a triangle is equal to the sum of the squares of the other two sides, then the angle opposite the first side is a right angle.
In $\triangle PQR$, the side PR is opposite to $\angle PQR$.
Therefore, we can conclude that $\angle PQR = 90^\circ$.
Hence Proved.
Question 12. Areas of two similar triangles are 36 cm2 and 100 cm2 . If the length of a side of the larger triangle is 20 cm, find the length of the corresponding side of the smaller triangle.
Answer:
Given:
Two triangles are similar.
Area of the smaller triangle ($\text{ar}_1$) = $36 \text{ cm}^2$.
Area of the larger triangle ($\text{ar}_2$) = $100 \text{ cm}^2$.
Length of a side of the larger triangle ($s_2$) = $20$ cm.
To Find:
The length of the corresponding side of the smaller triangle ($s_1$).
Solution:
We know that the ratio of the areas of two similar triangles is equal to the square of the ratio of their corresponding sides.
Let $s_1$ be the side of the smaller triangle and $s_2$ be the corresponding side of the larger triangle.
$\frac{\text{ar}_1}{\text{ar}_2} = \left(\frac{s_1}{s_2}\right)^2$
... (i)
Substitute the given values into this equation:
$\frac{36}{100} = \left(\frac{s_1}{20}\right)^2$
To solve for $s_1$, first take the square root of both sides of the equation:
$\sqrt{\frac{36}{100}} = \sqrt{\left(\frac{s_1}{20}\right)^2}$
$\frac{6}{10} = \frac{s_1}{20}$
Now, solve for $s_1$ by multiplying both sides by 20:
$s_1 = \frac{6}{10} \times 20$
$s_1 = 6 \times \frac{20}{10} = 6 \times 2$
$s_1 = 12$ cm
Final Answer:
The length of the corresponding side of the smaller triangle is 12 cm.
Question 13. In Fig. 6.12, if ∠ACB = ∠CDA, AC = 8 cm and AD = 3 cm, find BD.
Answer:
Given:
In the figure, we have a triangle ABC with a point D on the side AB.
The following are given:
$\angle ACB = \angle CDA$
$AC = 8$ cm
$AD = 3$ cm
To Find:
The length of the segment BD.
Solution:
To find the length of BD, we first need to establish a relationship between the triangles in the figure. Let's compare $\triangle ABC$ and $\triangle ACD$.
In $\triangle ABC$ and $\triangle ACD$:
$\angle BAC = \angle CAD$
(Common angle)
$\angle ACB = \angle CDA$
(Given)
Since two angles of $\triangle ABC$ are equal to two corresponding angles of $\triangle ACD$, the two triangles are similar by the AA (Angle-Angle) similarity criterion.
The correspondence of vertices is A $\leftrightarrow$ A, C $\leftrightarrow$ D, and B $\leftrightarrow$ C.
$\triangle ABC \sim \triangle ACD$
(By AA similarity)
Since the triangles are similar, the ratio of their corresponding sides must be equal:
$\frac{AB}{AC} = \frac{BC}{CD} = \frac{AC}{AD}$
Using the first and third parts of the ratio, which involve the known lengths, we have:
$\frac{AB}{AC} = \frac{AC}{AD}$
Substitute the given values $AC = 8$ cm and $AD = 3$ cm into the equation:
$\frac{AB}{8} = \frac{8}{3}$
Now, we can solve for the length of AB by cross-multiplication:
$AB = \frac{8 \times 8}{3} = \frac{64}{3}$ cm
From the figure, we can see that the side AB is composed of two segments, AD and BD.
$AB = AD + BD$
To find BD, we rearrange the equation:
$BD = AB - AD$
Substitute the values of AB and AD:
$BD = \frac{64}{3} - 3$
$BD = \frac{64 - (3 \times 3)}{3} = \frac{64 - 9}{3}$
$BD = \frac{55}{3}$ cm
Final Answer:
The length of BD is $\frac{55}{3}$ cm.
Question 14. A 15 metres high tower casts a shadow 24 metres long at a certain time and at the same time, a telephone pole casts a shadow 16 metres long. Find the height of the telephone pole.
Answer:
Given:
Height of the tower ($H_T$) = $15$ metres.
Length of the shadow of the tower ($S_T$) = $24$ metres.
Length of the shadow of the telephone pole ($S_P$) = $16$ metres.
To Find:
The height of the telephone pole ($H_P$).
Solution:
At a particular time, the rays of the sun are parallel. This means the angle of elevation of the sun for both the tower and the telephone pole will be the same.
Let the tower be represented by AB and its shadow by BC. Let the telephone pole be represented by PQ and its shadow by QR.
In $\triangle ABC$ and $\triangle PQR$:
Both the tower and the pole are assumed to be standing vertically on the ground. Therefore,
$\angle ABC = \angle PQR = 90^\circ$
(Vertical objects)
The angle of elevation of the sun is the same for both.
$\angle ACB = \angle PRQ$
(Same angle of elevation)
By the AA (Angle-Angle) similarity criterion, the two triangles are similar.
$\triangle ABC \sim \triangle PQR$
Since the triangles are similar, the ratio of their corresponding sides is equal.
$\frac{AB}{PQ} = \frac{BC}{QR}$
Substituting the given terms:
$\frac{H_T}{H_P} = \frac{S_T}{S_P}$
Now, substitute the numerical values:
$\frac{15}{H_P} = \frac{24}{16}$
Simplify the fraction on the right side:
$\frac{15}{H_P} = \frac{\cancel{24}^{3}}{\cancel{16}_{2}} = \frac{3}{2}$
Now, solve for $H_P$ by cross-multiplication:
$15 \times 2 = 3 \times H_P$
$30 = 3 \times H_P$
$H_P = \frac{30}{3} = 10$ metres
Final Answer:
The height of the telephone pole is 10 metres.
Question 15. Foot of a 10 m long ladder leaning against a vertical wall is 6 m away from the base of the wall. Find the height of the point on the wall where the top of the ladder reaches.
Answer:
Given:
Length of the ladder = $10$ m.
Distance between the foot of the ladder and the base of the wall = $6$ m.
To Find:
The height of the point on the wall where the top of the ladder reaches.
Solution:
The ladder, the wall, and the ground form a right-angled triangle. The wall is perpendicular to the ground, and the ladder acts as the hypotenuse.
Let:
$h$ = the height on the wall where the ladder reaches (perpendicular).
$b$ = the distance from the base of the wall to the foot of the ladder (base) = $6$ m.
$l$ = the length of the ladder (hypotenuse) = $10$ m.
According to the Pythagorean theorem, in a right-angled triangle:
$(\text{Perpendicular})^2 + (\text{Base})^2 = (\text{Hypotenuse})^2$
$h^2 + b^2 = l^2$
Substitute the given values into the equation:
$h^2 + 6^2 = 10^2$
Calculate the squares:
$h^2 + 36 = 100$
To find $h^2$, subtract 36 from both sides of the equation:
$h^2 = 100 - 36$
$h^2 = 64$
To find $h$, take the square root of both sides (since height must be positive):
$h = \sqrt{64} = 8$ m
Final Answer:
The height of the point on the wall where the top of the ladder reaches is 8 m.
Sample Question 1 to 4 (Before Exercise 6.4)
Sample Question 1: In Fig 6.13, OB is the perpendicular bisector of the line segment DE, FA ⊥OB and F E intersects OB at the point C. Prove that $\frac{1}{OA}$ + $\frac{1}{OB}$ = $\frac{2}{OC}$ .
Answer:
Given:
In Fig 6.13, OB is the perpendicular bisector of the line segment DE.
This implies that $DB = BE$ and $OB \perp DE$ (so $\angle OBD = 90^\circ$).
We are also given that $FA \perp OB$, which implies $\angle OAF = 90^\circ$.
FE intersects OB at point C.
To Prove:
$\frac{1}{OA} + \frac{1}{OB} = \frac{2}{OC}$
Proof:
Consider $\triangle AOF$ and $\triangle BOD$.
$\angle AOF = \angle BOD$
(Common angle, also denoted as $\angle O$)
$\angle FAO = \angle DBO = 90^\circ$
(Given)
By AA (Angle-Angle) similarity criterion, the two triangles are similar.
$\triangle AOF \sim \triangle BOD$
Therefore, the ratio of their corresponding sides is equal.
$\frac{OA}{OB} = \frac{FA}{DB}$
... (i)
Now, consider $\triangle FAC$ and $\triangle EBC$.
$\angle FAC = \angle EBC = 90^\circ$
(Given)
$\angle FCA = \angle ECB$
(Vertically opposite angles)
By AA similarity criterion, the two triangles are similar.
$\triangle FAC \sim \triangle EBC$
Therefore, the ratio of their corresponding sides is equal.
$\frac{FA}{EB} = \frac{AC}{BC}$
Since OB is the perpendicular bisector of DE, B is the midpoint of DE. Thus, $EB = DB$.
Substituting $EB$ with $DB$ in the above ratio:
$\frac{FA}{DB} = \frac{AC}{BC}$
... (ii)
From equations (i) and (ii), we can equate the expressions for $\frac{FA}{DB}$:
$\frac{OA}{OB} = \frac{AC}{BC}$
From the figure, we can express AC and BC in terms of OA, OB, and OC:
$AC = OC - OA$
$BC = OB - OC$
Substituting these into the equation:
$\frac{OA}{OB} = \frac{OC - OA}{OB - OC}$
Now, we cross-multiply:
$OA (OB - OC) = OB (OC - OA)$
$OA \cdot OB - OA \cdot OC = OB \cdot OC - OB \cdot OA$
Rearrange the terms to bring similar terms together:
$OA \cdot OB + OB \cdot OA = OB \cdot OC + OA \cdot OC$
$2 OA \cdot OB = OC (OB + OA)$
To get the desired result, divide both sides of the equation by $(OA \cdot OB \cdot OC)$:
$\frac{2 OA \cdot OB}{OA \cdot OB \cdot OC} = \frac{OC (OB + OA)}{OA \cdot OB \cdot OC}$
$\frac{2}{OC} = \frac{OB + OA}{OA \cdot OB}$
$\frac{2}{OC} = \frac{OB}{OA \cdot OB} + \frac{OA}{OA \cdot OB}$
$\frac{2}{OC} = \frac{1}{OA} + \frac{1}{OB}$
Rearranging this gives the final expression:
$\frac{1}{OA} + \frac{1}{OB} = \frac{2}{OC}$
Hence, Proved.
Sample Question 2: Prove that if in a triangle square on one side is equal to the sum of the squares on the other two sides, then the angle opposite the first side is a right angle.
Answer:
This theorem is the Converse of the Pythagorean Theorem.
Given:
In a triangle $\triangle ABC$, the square of side AC is equal to the sum of the squares of the other two sides, AB and BC.
$AC^2 = AB^2 + BC^2$
... (i)
To Prove:
The angle opposite to the side AC, which is $\angle B$, is a right angle.
i.e., $\angle B = 90^\circ$.
Construction Required:
Construct a right-angled triangle $\triangle PQR$, right-angled at Q, such that its sides PQ and QR are equal to the sides AB and BC of $\triangle ABC$, respectively.
$PQ = AB$
(By construction)
$QR = BC$
(By construction)
$\angle Q = 90^\circ$
(By construction)
Proof:
In the constructed $\triangle PQR$, since $\angle Q = 90^\circ$, we can apply the Pythagorean Theorem.
$PR^2 = PQ^2 + QR^2$
[By Pythagorean Theorem] ... (ii)
By construction, we have $PQ = AB$ and $QR = BC$. Substituting these into equation (ii):
$PR^2 = AB^2 + BC^2$
... (iii)
From the given information (equation (i)), we have:
$AC^2 = AB^2 + BC^2$
Comparing equations (i) and (iii), the right-hand sides are identical. Therefore, the left-hand sides must be equal.
$AC^2 = PR^2$
[From (i) and (iii)]
Taking the square root on both sides (since length must be positive):
$AC = PR$
... (iv)
Now, let's compare $\triangle ABC$ and $\triangle PQR$.
$AB = PQ$
(By construction)
$BC = QR$
(By construction)
$AC = PR$
(Proved in (iv))
Since all three corresponding sides of the triangles are equal, the two triangles are congruent by the SSS (Side-Side-Side) congruence criterion.
$\triangle ABC \cong \triangle PQR$
[By SSS congruence]
Since the triangles are congruent, their corresponding angles are equal (CPCTC).
$\angle B = \angle Q$
(CPCTC)
From our construction, we know that $\angle Q = 90^\circ$.
Therefore, $\angle B = 90^\circ$.
Hence, Proved.
Sample Question 3: An aeroplane leaves an Airport and flies due North at 300 km/h. At the same time, another aeroplane leaves the same Airport and flies due West at 400 km/h. How far apart the two aeroplanes would be after $1\frac{1}{2}$ hours?
Answer:
Given:
Speed of the first aeroplane (flying due North) = $300$ km/h.
Speed of the second aeroplane (flying due West) = $400$ km/h.
Both aeroplanes fly for the same duration of time.
Time = $1\frac{1}{2} \text{ hours} = 1.5 \text{ hours}$.
To Find:
The distance between the two aeroplanes after $1.5$ hours.
Solution:
Let the Airport be at the origin O.
The first aeroplane flies due North. Let its position after $1.5$ hours be A.
The second aeroplane flies due West. Let its position after $1.5$ hours be B.
We calculate the distance covered by each aeroplane using the formula: Distance = Speed × Time.
Distance covered by the first aeroplane (flying North):
$OA = 300 \text{ km/h} \times 1.5 \text{ h} = 450$ km
Distance covered by the second aeroplane (flying West):
$OB = 400 \text{ km/h} \times 1.5 \text{ h} = 600$ km
Since one aeroplane flies North and the other flies West from the same point, their paths are perpendicular to each other. Therefore, the angle between their paths, $\angle AOB$, is $90^\circ$.
This forms a right-angled triangle $\triangle AOB$, with the right angle at O. The distance between the two aeroplanes, AB, is the hypotenuse of this triangle.
Using the Pythagorean Theorem:
$AB^2 = OA^2 + OB^2$
Substitute the calculated distances:
$AB^2 = (450)^2 + (600)^2$
$AB^2 = 202500 + 360000$
$AB^2 = 562500$
To find the distance AB, we take the square root of both sides:
$AB = \sqrt{562500} = \sqrt{750 \times 750}$
$AB = 750$ km
Final Answer:
The two aeroplanes would be 750 km apart after $1\frac{1}{2}$ hours.
Sample Question 4: In Fig. 6.15, if ΔABC ~ ΔDEF and their sides are of lengths (in cm) as marked along them, then find the lengths of the sides of each triangle.
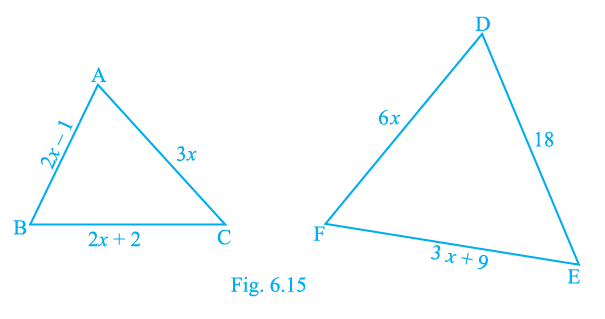
Answer:
Given:
$\triangle ABC \sim \triangle DEF$
Side lengths of $\triangle ABC$: AB = $2x - 1$, BC = $2x + 2$, AC = $3x$.
Side lengths of $\triangle DEF$: DE = $18$, EF = $3x + 9$, DF = $6x$.
To Find:
The lengths of the sides of $\triangle ABC$ and $\triangle DEF$.
Solution:
Since $\triangle ABC \sim \triangle DEF$, the ratio of their corresponding sides is equal.
$\underbrace{\frac{AB}{DE} = \frac{BC}{EF} = \frac{AC}{DF}}_{\text{Property of similar triangles}}$
Substitute the given side lengths into the ratio:
$\frac{2x - 1}{18} = \frac{2x + 2}{3x + 9} = \frac{3x}{6x}$
Let's simplify the third ratio $\frac{3x}{6x}$. Assuming $x \neq 0$, we get:
$\frac{3x}{6x} = \frac{\cancel{3x}}{\cancel{6x}^2} = \frac{1}{2}$
Now, we can equate any of the first two ratios to $\frac{1}{2}$ to find the value of $x$. Let's use the first ratio:
$\frac{2x - 1}{18} = \frac{1}{2}$
Multiply both sides by 18:
$(2x - 1) = \frac{1}{2} \times 18$
$2x - 1 = 9$
Add 1 to both sides:
$2x = 9 + 1$
$2x = 10$
Divide by 2:
$x = \frac{10}{2}$
$x = 5$
Now, substitute the value of $x=5$ into the expressions for the side lengths of both triangles.
Sides of $\triangle ABC$:
AB = $2x - 1 = 2(5) - 1 = 10 - 1 = 9$ cm
BC = $2x + 2 = 2(5) + 2 = 10 + 2 = 12$ cm
AC = $3x = 3(5) = 15$ cm
Sides of $\triangle DEF$:
DE = $18$ cm
EF = $3x + 9 = 3(5) + 9 = 15 + 9 = 24$ cm
DF = $6x = 6(5) = 30$ cm
The lengths of the sides of $\triangle ABC$ are 9 cm, 12 cm, and 15 cm.
The lengths of the sides of $\triangle DEF$ are 18 cm, 24 cm, and 30 cm.
Exercise 6.4
Question 1. In Fig. 6.16, if∠A =∠C, AB = 6 cm, BP = 15 cm, AP = 12 cm and CP = 4 cm, then find the lengths of PD and CD.
Answer:
Given:
In the given figure, we have two triangles $\triangle APB$ and $\triangle CPD$.
$\angle A = \angle C$
AB = 6 cm
BP = 15 cm
AP = 12 cm
CP = 4 cm
To Find:
The lengths of PD and CD.
Solution:
Consider triangles $\triangle APB$ and $\triangle CPD$.
$\angle A = \angle C$
(Given)
$\angle APB = \angle CPD$
(Vertically Opposite Angles)
Since two angles of $\triangle APB$ are equal to two corresponding angles of $\triangle CPD$, by the AA (Angle-Angle) Similarity Criterion, we can say that $\triangle APB$ is similar to $\triangle CPD$.
Note the order of vertices in the similarity statement corresponds to the equal angles: A maps to C, P maps to P, and B maps to D.
So, we have $\triangle APB \sim \triangle CPD$.
When two triangles are similar, the ratio of their corresponding sides is equal.
$\underbrace{\frac{AP}{CP} = \frac{PB}{PD} = \frac{AB}{CD}}_{\text{Corresponding sides of similar triangles are proportional}}$
Substitute the given values into the ratios:
$\frac{12}{4} = \frac{15}{PD} = \frac{6}{CD}$
Simplify the first ratio:
$\frac{12}{4} = 3$
Now equate the ratios involving the unknowns to the simplified ratio 3.
For PD:
$\frac{15}{PD} = 3$
$15 = 3 \times PD$
$PD = \frac{15}{3}$
$PD = 5$ cm
For CD:
$\frac{6}{CD} = 3$
$6 = 3 \times CD$
$CD = \frac{6}{3}$
$CD = 2$ cm
The length of PD is 5 cm and the length of CD is 2 cm.
Question 2. It is given that ΔABC ~ ΔEDF such that AB = 5 cm, AC = 7 cm, DF = 15 cm and DE = 12 cm. Find the lengths of the remaining sides of the triangles.
Answer:
Given:
We are given that $\triangle ABC$ is similar to $\triangle EDF$ ($\triangle ABC \sim \triangle EDF$).
The lengths of the known sides are:
$AB = 5$ cm
$AC = 7$ cm
$DF = 15$ cm
$DE = 12$ cm
To Find:
The lengths of the remaining sides of the triangles, which are BC and EF.
Solution:
Since $\triangle ABC \sim \triangle EDF$, the ratio of their corresponding sides must be equal.
From the similarity statement, the corresponding vertices are A $\leftrightarrow$ E, B $\leftrightarrow$ D, and C $\leftrightarrow$ F.
Therefore, the corresponding sides are AB and ED, BC and DF, and AC and EF.
We can set up the following proportion:
$\frac{AB}{ED} = \frac{BC}{DF} = \frac{AC}{EF}$
... (i)
Now, substitute the given values into this proportion:
$\frac{5}{12} = \frac{BC}{15} = \frac{7}{EF}$
We can use this relationship to solve for the unknown lengths BC and EF.
To find the length of BC:
We use the first two parts of the proportion:
$\frac{5}{12} = \frac{BC}{15}$
By cross-multiplication:
$BC = \frac{5 \times 15}{12} = \frac{75}{12}$
Simplifying the fraction:
$BC = \frac{25}{4} = 6.25$ cm
To find the length of EF:
We use the first and third parts of the proportion:
$\frac{5}{12} = \frac{7}{EF}$
By cross-multiplication:
$5 \times EF = 12 \times 7$
$EF = \frac{84}{5} = 16.8$ cm
Final Answer:
The lengths of the remaining sides are BC = 6.25 cm and EF = 16.8 cm.
Question 3. Prove that if a line is drawn parallel to one side of a triangle to intersect the other two sides, then the two sides are divided in the same ratio.
Answer:
This theorem is known as the Basic Proportionality Theorem (BPT) or Thales' Theorem.
Given:
A triangle $\triangle ABC$ in which a line segment DE is drawn parallel to the side BC, intersecting the sides AB and AC at points D and E respectively.
DE || BC
To Prove:
The line DE divides the sides AB and AC in the same ratio. That is:
$\frac{AD}{DB} = \frac{AE}{EC}$
Construction Required:
Join the vertices B to E and C to D. Also, draw a perpendicular from E to the side AB, let it be EM. Draw a perpendicular from D to the side AC, let it be DN.
$EM \perp AB$ and $DN \perp AC$.
Proof:
The area of a triangle is given by the formula: Area = $\frac{1}{2} \times \text{base} \times \text{height}$.
Considering $\triangle ADE$, with base AD, the height is EM.
$\text{ar}(\triangle ADE) = \frac{1}{2} \times AD \times EM$
Considering $\triangle BDE$, with base DB, the height is also EM.
$\text{ar}(\triangle BDE) = \frac{1}{2} \times DB \times EM$
Now, let's find the ratio of their areas:
$\frac{\text{ar}(\triangle ADE)}{\text{ar}(\triangle BDE)} = \frac{\frac{1}{2} \times AD \times EM}{\frac{1}{2} \times DB \times EM} = \frac{AD}{DB}$
... (i)
Similarly, considering $\triangle ADE$ with base AE, the height is DN.
$\text{ar}(\triangle ADE) = \frac{1}{2} \times AE \times DN$
And considering $\triangle CDE$ with base EC, the height is also DN.
$\text{ar}(\triangle CDE) = \frac{1}{2} \times EC \times DN$
The ratio of their areas is:
$\frac{\text{ar}(\triangle ADE)}{\text{ar}(\triangle CDE)} = \frac{\frac{1}{2} \times AE \times DN}{\frac{1}{2} \times EC \times DN} = \frac{AE}{EC}$
... (ii)
Now, observe that $\triangle BDE$ and $\triangle CDE$ are on the same base DE and lie between the same parallel lines DE and BC.
A property of triangles states that triangles on the same base and between the same parallels are equal in area.
$\text{ar}(\triangle BDE) = \text{ar}(\triangle CDE)$
(Triangles on same base and between same parallels) ... (iii)
From equations (i), (ii), and (iii), we can conclude that the left-hand sides of (i) and (ii) are equal, because their denominators are equal.
$\frac{\text{ar}(\triangle ADE)}{\text{ar}(\triangle BDE)} = \frac{\text{ar}(\triangle ADE)}{\text{ar}(\triangle CDE)}$
Therefore, their right-hand sides must also be equal.
$\frac{AD}{DB} = \frac{AE}{EC}$
Hence, Proved.
Question 4. In Fig 6.17, if PQRS is a parallelogram and AB || PS, then prove that OC || SR.
Answer:
Given:
In the given figure, PQRS is a parallelogram. This means:
$PS \parallel QR$ and $PQ \parallel SR$.
We are also given that $AB \parallel PS$.
Since $AB \parallel PS$ and $PS \parallel QR$, we can conclude that $AB \parallel PS \parallel QR$.
To prove:
$OC \parallel SR$.
Proof:
First, consider the triangles $\triangle OPS$ and $\triangle OAB$.
Since $PS \parallel AB$ (Given), and OB is a transversal:
$\angle OSP = \angle OBA$
(Corresponding angles)
Also, the angle at vertex O is common to both triangles.
$\angle POS = \angle AOB$
(Common angle)
By the AA (Angle-Angle) similarity criterion, the two triangles are similar.
$\triangle OPS \sim \triangle OAB$
Therefore, the ratio of their corresponding sides is equal:
$\frac{PS}{AB} = \frac{OS}{OB}$
... (i)
Next, consider the triangles $\triangle CQR$ and $\triangle CAB$.
Since $QR \parallel AB$ (Proved above), and CB is a transversal:
$\angle CRQ = \angle CBA$
(Corresponding angles)
The angle at vertex C is common to both triangles.
$\angle QCR = \angle ACB$
(Common angle)
By the AA (Angle-Angle) similarity criterion, these two triangles are also similar.
$\triangle CQR \sim \triangle CAB$
Therefore, the ratio of their corresponding sides is equal:
$\frac{QR}{AB} = \frac{CR}{CB}$
... (ii)
Since PQRS is a parallelogram, its opposite sides are equal in length.
$PS = QR$
(Opposite sides of a parallelogram)
From equations (i) and (ii), using the fact that $PS = QR$, we can equate the ratios:
$\frac{OS}{OB} = \frac{CR}{CB}$
... (iii)
Taking the reciprocal of both sides:
$\frac{OB}{OS} = \frac{CB}{CR}$
Subtracting 1 from both sides (property of ratios - dividendo):
$\frac{OB}{OS} - 1 = \frac{CB}{CR} - 1$
$\frac{OB - OS}{OS} = \frac{CB - CR}{CR}$
From the figure, we can see that $OB - OS = BS$ and $CB - CR = BR$.
$\frac{BS}{OS} = \frac{BR}{CR}$
Now, consider the triangle $\triangle BOC$. The line segment SR intersects the sides BO at S and BC at R.
Since the line segment SR divides the sides BO and BC in the same ratio, i.e., $\frac{BS}{SO} = \frac{BR}{RC}$, by the Converse of the Basic Proportionality Theorem, the line segment SR is parallel to the third side OC.
$SR \parallel OC$
Hence, Proved.
Question 5. A 5 m long ladder is placed leaning towards a vertical wall such that it reaches the wall at a point 4 m high. If the foot of the ladder is moved 1.6 m towards the wall, then find the distance by which the top of the ladder would slide upwards on the wall.
Answer:
Given:
Length of the ladder = $5$ m.
Initial height the ladder reaches on the wall = $4$ m.
The foot of the ladder is moved $1.6$ m towards the wall.
To Find:
The distance the top of the ladder slides upwards on the wall.
Solution:
Step 1: Find the initial distance of the foot of the ladder from the wall.
Let the ladder be AC, the wall be AB, and the ground be BC. This forms a right-angled triangle ABC, right-angled at B.
Given:
Length of the ladder, AC = $5$ m.
Initial height on the wall, AB = $4$ m.
Let the initial distance of the foot from the wall be BC.
By the Pythagorean theorem in $\triangle ABC$:
$AC^2 = AB^2 + BC^2$
$5^2 = 4^2 + BC^2$
$25 = 16 + BC^2$
$BC^2 = 25 - 16 = 9$
$BC = \sqrt{9} = 3$ m
Step 2: Find the new height reached by the ladder.
The foot of the ladder is moved $1.6$ m towards the wall. Let the new position of the foot be E.
New distance from the wall, BE = BC - CE = $3 - 1.6 = 1.4$ m.
Let the new position of the top of the ladder on the wall be D. The ladder is now DE.
The length of the ladder remains the same, so DE = $5$ m.
Let the new height on the wall be DB.
By the Pythagorean theorem in the new right-angled triangle DBE:
$DE^2 = DB^2 + BE^2$
$5^2 = DB^2 + (1.4)^2$
$25 = DB^2 + 1.96$
$DB^2 = 25 - 1.96 = 23.04$
$DB = \sqrt{23.04} = 4.8$ m
Step 3: Calculate the distance the ladder slid upwards.
The distance the ladder slid upwards is the difference between the new height and the initial height.
Distance slid = New height (DB) - Initial height (AB)
$Distance = 4.8 \text{ m} - 4 \text{ m} = 0.8$ m
Final Answer:
The top of the ladder would slide upwards by $0.8$ m.
Question 6. For going to a city B from city A, there is a route via city C such that AC⊥CB, AC = 2 x km and CB = 2 (x + 7) km. It is proposed to construct a 26 km highway which directly connects the two cities A and B. Find how much distance will be saved in reaching city B from city A after the construction of the highway
Answer:
Given:
A route from city A to city B via city C forms a right-angled triangle.
The route AC is perpendicular to the route CB ($AC \perp CB$).
Length of AC = $2x$ km.
Length of CB = $2(x+7)$ km.
A direct highway AB is constructed with a length of $26$ km.
To Find:
The distance saved by using the direct highway instead of the route via city C.
Solution:
Step 1: Find the value of x.
Since $\triangle ACB$ is a right-angled triangle, we can apply the Pythagorean theorem:
$AC^2 + CB^2 = AB^2$
Substitute the given expressions:
$(2x)^2 + [2(x+7)]^2 = 26^2$
$4x^2 + 4(x+7)^2 = 676$
Expand $(x+7)^2$: $(x^2 + 14x + 49)$
$4x^2 + 4(x^2 + 14x + 49) = 676$
$4x^2 + 4x^2 + 56x + 196 = 676$
$8x^2 + 56x + 196 - 676 = 0$
$8x^2 + 56x - 480 = 0$
Divide the entire equation by 8 to simplify:
$x^2 + 7x - 60 = 0$
Factor the quadratic equation. We need two numbers that multiply to -60 and add to +7. The numbers are +12 and -5.
$(x+12)(x-5) = 0$
The possible solutions are $x = -12$ or $x = 5$. Since distance cannot be negative, we take $x = 5$.
Step 2: Calculate the length of the route via city C.
Using $x=5$:
$AC = 2x = 2(5) = 10$ km.
$CB = 2(x+7) = 2(5+7) = 2(12) = 24$ km.
Total distance via city C = $AC + CB = 10 + 24 = 34$ km.
Step 3: Calculate the distance saved.
Distance of the direct highway = $26$ km.
Distance saved = (Distance via city C) - (Distance of highway)
$Distance\ saved = 34 \text{ km} - 26 \text{ km} = 8$ km
Final Answer:
The distance saved in reaching city B from city A after the construction of the highway is $8$ km.
Question 7. A flag pole 18 m high casts a shadow 9.6 m long. Find the distance of the top of the pole from the far end of the shadow.
Answer:
Given:
Height of the flag pole = $18$ m.
Length of the shadow = $9.6$ m.
To Find:
The distance from the top of the pole to the far end of the shadow.
Solution:
The flag pole, its shadow, and the line connecting the top of the pole to the tip of the shadow form a right-angled triangle.
Let the height of the pole be the perpendicular, $p = 18$ m.
Let the length of the shadow be the base, $b = 9.6$ m.
The distance to be found is the hypotenuse, $h$.
By the Pythagorean theorem:
$p^2 + b^2 = h^2$
Substitute the given values:
$18^2 + (9.6)^2 = h^2$
$324 + 92.16 = h^2$
$h^2 = 416.16$
To find $h$, take the square root of both sides:
$h = \sqrt{416.16}$
We can calculate the square root: $\sqrt{416.16} = 20.4$.
$h = 20.4$ m
Final Answer:
The distance of the top of the pole from the far end of the shadow is $20.4$ m.
Question 8. A street light bulb is fixed on a pole 6 m above the level of the street. If a woman of height 1.5 m casts a shadow of 3m, find how far she is away from the base of the pole.
Answer:
Given:
Height of the pole with the street light (AB) = $6$ m.
Height of the woman (CD) = $1.5$ m.
Length of the woman's shadow (DE) = $3$ m.
To Find:
The distance of the woman from the base of the pole (BD).
Solution:
Let's visualize the scenario. The street light at A, the top of the woman's head at C, and the tip of her shadow at E form a straight line.
This setup creates two right-angled triangles, $\triangle ABE$ and $\triangle CDE$.
Both the pole and the woman are standing vertically, so they are perpendicular to the ground.
$\angle ABE = \angle CDE = 90^\circ$
The angle at the tip of the shadow, $\angle E$, is common to both triangles.
$\angle AEB = \angle CED$
(Common angle)
Since two angles of $\triangle ABE$ are equal to two angles of $\triangle CDE$, the triangles are similar by the AA (Angle-Angle) similarity criterion.
$\triangle ABE \sim \triangle CDE$
Because the triangles are similar, the ratio of their corresponding sides is equal:
$\frac{AB}{CD} = \frac{BE}{DE}$
Let the distance of the woman from the base of the pole be $x$ meters. So, $BD = x$.
The total length from the base of the pole to the tip of the shadow is $BE = BD + DE = x + 3$.
Now, substitute the known values into the proportion:
$\frac{6}{1.5} = \frac{x+3}{3}$
Simplify the left side:
$4 = \frac{x+3}{3}$
Multiply both sides by 3 to solve for $x$:
$4 \times 3 = x + 3$
$12 = x + 3$
$x = 12 - 3 = 9$ m
Final Answer:
The woman is $9$ m away from the base of the pole.
Question 9. In Fig. 6.18, ABC is a triangle right angled at B and BD ⊥AC. If AD = 4 cm, and CD = 5 cm, find BD and AB.
Answer:
Given:
In $\triangle{\text{ABC}}$, $\angle{\text{B}} = 90^\circ$.
BD $\perp$ AC.
AD = $4$ cm.
CD = $5$ cm.
To Find:
Length of BD.
Length of AB.
Solution:
In a right-angled triangle, the altitude to the hypotenuse divides the triangle into two triangles that are similar to the original triangle and to each other.
Thus, $\triangle{\text{ADB}} \sim \triangle{\text{BDC}} \sim \triangle{\text{ABC}}$.
Considering the similarity between $\triangle{\text{ADB}}$ and $\triangle{\text{BDC}}$, the ratio of corresponding sides is equal:
$\frac{\text{AD}}{\text{BD}} = \frac{\text{BD}}{\text{CD}}$
Cross-multiplying, we get the geometric mean theorem for the altitude:
$BD^2 = AD \times CD$
Substitute the given values of AD and CD:
$BD^2 = 4 \times 5$
$BD^2 = 20$
$BD = \sqrt{20}$
$BD = \sqrt{4 \times 5}$
$BD = 2\sqrt{5}$ cm.
Now, we need to find the length of AB.
The length of the hypotenuse AC is the sum of AD and CD:
AC = AD + CD
AC = $4 + 5 = 9$ cm.
Considering the similarity between $\triangle{\text{ADB}}$ and $\triangle{\text{ABC}}$, the ratio of corresponding sides is equal:
$\frac{\text{AB}}{\text{AC}} = \frac{\text{AD}}{\text{AB}}$
Cross-multiplying, we get the geometric mean theorem for the leg:
$AB^2 = AD \times AC$
Substitute the values of AD and AC:
$AB^2 = 4 \times 9$
$AB^2 = 36$
$AB = \sqrt{36}$
$AB = 6$ cm.
Answer:
The length of BD is $2\sqrt{5}$ cm.
The length of AB is $6$ cm.
Question 10. In Fig. 6.19, PQR is a right triangle right angled at Q and QS ⊥ PR . If PQ = 6 cm and PS = 4 cm, find QS, RS and QR
Answer:
Given:
In $\triangle{\text{PQR}}$, $\angle{\text{Q}} = 90^\circ$.
QS $\perp$ PR.
PQ = $6$ cm.
PS = $4$ cm.
To Find:
Length of QS.
Length of RS.
Length of QR.
Solution:
In a right-angled triangle, the altitude to the hypotenuse divides the triangle into two triangles that are similar to the original triangle and to each other.
Thus, $\triangle{\text{PQS}} \sim \triangle{\text{RQS}} \sim \triangle{\text{PQR}}$.
Consider the similarity between $\triangle{\text{PQS}}$ and $\triangle{\text{PQR}}$. The ratio of corresponding sides is equal:
$\frac{\text{PQ}}{\text{PR}} = \frac{\text{PS}}{\text{PQ}}$
This gives $PQ^2 = PS \times PR$.
Substitute the given values PQ = $6$ and PS = $4$:
$6^2 = 4 \times PR$
$36 = 4 \times PR$
$PR = \frac{36}{4}$
$PR = 9$ cm.
Now that we have PR and PS, we can find RS:
RS = PR - PS
RS = $9 - 4$
RS = $5$ cm.
Now, consider the similarity between $\triangle{\text{PQS}}$ and $\triangle{\text{RQS}}$. The ratio of corresponding sides is equal:
$\frac{\text{QS}}{\text{RS}} = \frac{\text{PS}}{\text{QS}}$
This gives $QS^2 = PS \times RS$.
Substitute the values PS = $4$ and RS = $5$:
$QS^2 = 4 \times 5$
$QS^2 = 20$
$QS = \sqrt{20}$
$QS = \sqrt{4 \times 5}$
$QS = 2\sqrt{5}$ cm.
Finally, we need to find QR. Consider the similarity between $\triangle{\text{RQS}}$ and $\triangle{\text{PQR}}$. The ratio of corresponding sides is equal:
$\frac{\text{QR}}{\text{PR}} = \frac{\text{RS}}{\text{QR}}$
This gives $QR^2 = RS \times PR$.
Substitute the values RS = $5$ and PR = $9$:
$QR^2 = 5 \times 9$
$QR^2 = 45$
$QR = \sqrt{45}$
$QR = \sqrt{9 \times 5}$
$QR = 3\sqrt{5}$ cm.
Alternatively, QR can be found using the Pythagorean theorem in $\triangle{\text{RQS}}$:
$QS^2 + RS^2 = QR^2$
$(2\sqrt{5})^2 + 5^2 = QR^2$
$20 + 25 = QR^2$
$45 = QR^2$
$QR = \sqrt{45} = 3\sqrt{5}$ cm. (This confirms the result)
Answer:
The length of QS is $2\sqrt{5}$ cm.
The length of RS is $5$ cm.
The length of QR is $3\sqrt{5}$ cm.
Question 11. In PQR, PD ⊥ QR such that D lies on QR . If PQ = a, PR = b, QD = c and DR = d, prove that (a + b) (a – b) = (c + d) (c – d).
Answer:
Given:
In $\triangle PQR$, an altitude PD is drawn to the side QR, so $PD \perp QR$.
The lengths of the segments are given as:
$PQ = a$
$PR = b$
$QD = c$
$DR = d$
To Prove:
$(a + b) (a – b) = (c + d) (c – d)$
Proof:
Since $PD \perp QR$, it divides $\triangle PQR$ into two right-angled triangles: $\triangle PDQ$ and $\triangle PDR$.
In the right-angled triangle $\triangle PDQ$, by the Pythagorean theorem:
$PQ^2 = PD^2 + QD^2$
Substituting the given values:
$a^2 = PD^2 + c^2$
From this, we can express $PD^2$ as:
$PD^2 = a^2 - c^2$
... (i)
In the right-angled triangle $\triangle PDR$, by the Pythagorean theorem:
$PR^2 = PD^2 + DR^2$
Substituting the given values:
$b^2 = PD^2 + d^2$
From this, we can also express $PD^2$ as:
$PD^2 = b^2 - d^2$
... (ii)
From equations (i) and (ii), since both are expressions for $PD^2$, we can equate them:
$a^2 - c^2 = b^2 - d^2$
Rearrange the terms to group 'a' and 'b' on one side, and 'c' and 'd' on the other:
$a^2 - b^2 = c^2 - d^2$
Using the algebraic identity for the difference of squares, $x^2 - y^2 = (x + y)(x - y)$, we can factor both sides of the equation:
$(a + b)(a - b) = (c + d)(c - d)$
Hence Proved.
Question 12. In a quadrilateral ABCD, ∠A + ∠D = 90°. Prove that AC2 + BD2 = AD2 + BC2
[Hint: Produce AB and DC to meet at E.]
Answer:
Given:
A quadrilateral ABCD with the property that the sum of two adjacent angles is $90^\circ$.
$\angle A + \angle D = 90^\circ$
To Prove:
$AC^2 + BD^2 = AD^2 + BC^2$
Construction Required:
Produce the sides AB and DC to meet at a point E.
Proof:
Consider the triangle $\triangle ADE$ formed by the construction.
The sum of the angles in any triangle is $180^\circ$.
In $\triangle ADE$:
$\angle EAD + \angle ADE + \angle AED = 180^\circ$
Here, $\angle EAD = \angle A$ and $\angle ADE = \angle D$ of the quadrilateral.
$\angle A + \angle D + \angle AED = 180^\circ$
We are given that $\angle A + \angle D = 90^\circ$. Substituting this into the equation:
$90^\circ + \angle AED = 180^\circ$
$\angle AED = 180^\circ - 90^\circ = 90^\circ$
This means that $\triangle ADE$ is a right-angled triangle with the right angle at E. Consequently, any triangle with E as a vertex within this construction (like $\triangle BCE, \triangle ACE, \triangle BDE$) is also right-angled at E.
Now, we apply the Pythagorean theorem to the four right-angled triangles:
1. In $\triangle ACE$: $AC^2 = AE^2 + CE^2$
2. In $\triangle BDE$: $BD^2 = BE^2 + DE^2$
3. In $\triangle ADE$: $AD^2 = AE^2 + DE^2$
4. In $\triangle BCE$: $BC^2 = BE^2 + CE^2$
We want to prove $AC^2 + BD^2 = AD^2 + BC^2$. Let's evaluate the Left Hand Side (LHS) and Right Hand Side (RHS) separately.
LHS = $AC^2 + BD^2$
Substituting the expressions from Pythagorean theorem:
$LHS = (AE^2 + CE^2) + (BE^2 + DE^2)$
RHS = $AD^2 + BC^2$
Substituting the expressions from Pythagorean theorem:
$RHS = (AE^2 + DE^2) + (BE^2 + CE^2)$
By rearranging the terms, we can see that:
$LHS = AE^2 + BE^2 + CE^2 + DE^2$
$RHS = AE^2 + BE^2 + CE^2 + DE^2$
Since LHS = RHS, the original statement is true.
$AC^2 + BD^2 = AD^2 + BC^2$
Hence Proved.
Question 13. In fig. 6.20, l || m and line segments AB, CD and EF are concurrent at point P. Prove that $\frac{AE}{BF}$ = $\frac{AC}{BD}$ = $\frac{CE}{FD}$ .
Answer:
Given:
Lines l and m are parallel ($l || m$).
Line segments AB, CD, and EF intersect at point P.
Points A, C, E lie on line l, and points B, D, F lie on line m.
To Prove:
$\frac{AE}{BF} = \frac{AC}{BD} = \frac{CE}{FD}$.
Proof:
Consider the triangles $\triangle{\text{PAC}}$ and $\triangle{\text{PBD}}$.
$\angle{\text{APC}} = \angle{\text{BPD}}$ (Vertically opposite angles)
Since line l || line m and AB is a transversal, $\angle{\text{PAC}} = \angle{\text{PBD}}$ (Alternate interior angles)
Therefore, $\triangle{\text{PAC}} \sim \triangle{\text{PBD}}$ by AA similarity criterion.
Since the triangles are similar, the ratio of their corresponding sides is equal:
$\frac{\text{PA}}{\text{PB}} = \frac{\text{PC}}{\text{PD}} = \frac{\text{AC}}{\text{BD}}$
Consider the triangles $\triangle{\text{PAE}}$ and $\triangle{\text{PBF}}$.
$\angle{\text{APE}} = \angle{\text{BPF}}$ (Vertically opposite angles)
Since line l || line m and EF is a transversal, $\angle{\text{PAE}} = \angle{\text{PBF}}$ (Alternate interior angles)
Therefore, $\triangle{\text{PAE}} \sim \triangle{\text{PBF}}$ by AA similarity criterion.
Since the triangles are similar, the ratio of their corresponding sides is equal:
$\frac{\text{PA}}{\text{PB}} = \frac{\text{PE}}{\text{PF}} = \frac{\text{AE}}{\text{BF}}$
Consider the triangles $\triangle{\text{PCE}}$ and $\triangle{\text{PFD}}$.
$\angle{\text{CPE}} = \angle{\text{DPF}}$ (Vertically opposite angles)
Since line l || line m and CD is a transversal, $\angle{\text{PCE}} = \angle{\text{PFD}}$ (Alternate interior angles)
Therefore, $\triangle{\text{PCE}} \sim \triangle{\text{PFD}}$ by AA similarity criterion.
Since the triangles are similar, the ratio of their corresponding sides is equal:
$\frac{\text{PC}}{\text{PD}} = \frac{\text{PE}}{\text{PF}} = \frac{\text{CE}}{\text{FD}}$
From the similarity of $\triangle{\text{PAC}}$ and $\triangle{\text{PBD}}$, we have $\frac{\text{AC}}{\text{BD}} = \frac{\text{PA}}{\text{PB}}$.
From the similarity of $\triangle{\text{PAE}}$ and $\triangle{\text{PBF}}$, we have $\frac{\text{AE}}{\text{BF}} = \frac{\text{PA}}{\text{PB}}$.
Equating the ratios involving $\frac{\text{PA}}{\text{PB}}$ from these two similarities, we get:
$\frac{\text{AE}}{\text{BF}} = \frac{\text{AC}}{\text{BD}}$
From the similarity of $\triangle{\text{PAC}}$ and $\triangle{\text{PBD}}$, we have $\frac{\text{AC}}{\text{BD}} = \frac{\text{PC}}{\text{PD}}$.
From the similarity of $\triangle{\text{PCE}}$ and $\triangle{\text{PFD}}$, we have $\frac{\text{CE}}{\text{FD}} = \frac{\text{PC}}{\text{PD}}$.
Equating the ratios involving $\frac{\text{PC}}{\text{PD}}$ from these two similarities, we get:
$\frac{\text{AC}}{\text{BD}} = \frac{\text{CE}}{\text{FD}}$
Combining the two results:
$\frac{\text{AE}}{\text{BF}} = \frac{\text{AC}}{\text{BD}}$ and $\frac{\text{AC}}{\text{BD}} = \frac{\text{CE}}{\text{FD}}$.
Therefore, we can conclude that:
$\frac{AE}{BF} = \frac{AC}{BD} = \frac{CE}{FD}$
This proves the required relationship between the line segments.
Hence Proved.
Question 14. In Fig. 6.21, PA, QB, RC and SD are all perpendiculars to a line l, AB = 6 cm, BC = 9 cm, CD = 12 cm and SP = 36 cm. Find PQ, QR and RS.
Answer:
Given:
PA, QB, RC, and SD are all perpendicular to a line $l$.
The lengths of the segments on line $l$ are:
$AB = 6$ cm
$BC = 9$ cm
$CD = 12$ cm
The total length of the transversal segment SP is:
$SP = 36$ cm
To Find:
The lengths of the segments PQ, QR, and RS.
Solution:
Since PA, QB, RC, and SD are all perpendicular to the same line $l$, they are all parallel to each other.
$PA \parallel QB \parallel RC \parallel SD$
We have a set of parallel lines intersected by two transversals, line $l$ (or AD) and line SP.
According to the Intercept Theorem (an extension of the Basic Proportionality Theorem), if three or more parallel lines are intersected by two transversals, they divide the transversals proportionally.
This means the ratio of the intercepts on one transversal is equal to the ratio of the corresponding intercepts on the other transversal.
Therefore, we can write:
$\frac{PQ}{AB} = \frac{QR}{BC} = \frac{RS}{CD}$
This also implies that the ratio of the segments PQ, QR, and RS is the same as the ratio of the segments AB, BC, and CD.
$PQ : QR : RS = AB : BC : CD$
Substituting the given values for AB, BC, and CD:
$PQ : QR : RS = 6 : 9 : 12$
We can simplify this ratio by dividing each part by their greatest common divisor, which is 3:
$PQ : QR : RS = 2 : 3 : 4$
Let the common ratio be $x$. Then we can write the lengths of the segments as:
$PQ = 2x$
$QR = 3x$
$RS = 4x$
The total length of the segment SP is the sum of these parts:
$SP = PQ + QR + RS$
We are given that $SP = 36$ cm. Substituting the values:
$36 = 2x + 3x + 4x$
$36 = 9x$
$x = \frac{36}{9} = 4$
Now we can find the lengths of PQ, QR, and RS by substituting $x=4$:
$PQ = 2x = 2(4) = 8$ cm
$QR = 3x = 3(4) = 12$ cm
$RS = 4x = 4(4) = 16$ cm
Final Answer:
The lengths of the segments are:
PQ = 8 cm
QR = 12 cm
RS = 16 cm
Question 15. O is the point of intersection of the diagonals AC and BD of a trapezium ABCD with AB || DC. Through O, a line segment PQ is drawn parallel to AB meeting AD in P and BC in Q. Prove that PO = QO.
Answer:
Given:
A trapezium ABCD in which $AB \parallel DC$.
The diagonals AC and BD intersect at point O.
A line segment PQ is drawn through O such that P is on AD, Q is on BC and $PQ \parallel AB$.
To Prove:
$PO = QO$.
Proof:
We are given that $AB \parallel DC$ and $PQ \parallel AB$.
Since lines parallel to the same line are parallel to each other, we have:
$AB \parallel DC \parallel PQ$.
Now, consider the triangle $\triangle ABD$.
Since P is on AD, O is on BD, and $PO \parallel AB$, by the property of similar triangles:
$\triangle DPO \sim \triangle DAB$
Therefore, the ratio of their corresponding sides is equal.
$\frac{PO}{AB} = \frac{DO}{DB}$
(Corresponding sides of similar triangles)
Rearranging this, we get:
$PO = AB \cdot \frac{DO}{DB}$
... (i)
Next, consider the triangle $\triangle BCD$.
Since Q is on BC, O is on BD, and $QO \parallel DC$, by the property of similar triangles:
$\triangle BQO \sim \triangle BCD$
Therefore, the ratio of their corresponding sides is equal.
$\frac{QO}{DC} = \frac{BO}{BD}$
(Corresponding sides of similar triangles)
Rearranging this, we get:
$QO = DC \cdot \frac{BO}{BD}$
... (ii)
Now, we need to find a relationship between the sides. Let's consider $\triangle AOB$ and $\triangle COD$.
$\angle OAB = \angle OCD$
(Alternate interior angles as $AB \parallel DC$)
$\angle OBA = \angle ODC$
(Alternate interior angles as $AB \parallel DC$)
By AA similarity criterion, $\triangle AOB \sim \triangle COD$.
So, the ratio of their corresponding sides is equal:
$\frac{AB}{DC} = \frac{BO}{DO}$
By cross-multiplication, we get:
$AB \cdot DO = DC \cdot BO$
... (iii)
From equation (i), we have $PO \cdot DB = AB \cdot DO$.
From equation (ii), we have $QO \cdot DB = DC \cdot BO$.
Using the result from equation (iii), we see that the right-hand sides of these two expressions are equal.
Therefore, their left-hand sides must also be equal.
$PO \cdot DB = QO \cdot DB$
Since DB is a diagonal, its length is not zero ($DB \neq 0$). We can divide both sides by DB.
$PO = QO$
Hence, Proved.
Alternate Solution
In $\triangle ADC$, since $PO \parallel DC$, by the property of similar triangles, $\triangle APO \sim \triangle ADC$.
$\frac{PO}{DC} = \frac{AP}{AD}$
... (a)
In $\triangle ADB$, since $PO \parallel AB$, by the property of similar triangles, $\triangle DPO \sim \triangle DAB$.
$\frac{PO}{AB} = \frac{DP}{AD}$
... (b)
Adding equations (a) and (b):
$\frac{PO}{DC} + \frac{PO}{AB} = \frac{AP}{AD} + \frac{DP}{AD}$
$PO \left( \frac{1}{DC} + \frac{1}{AB} \right) = \frac{AP+DP}{AD} = \frac{AD}{AD} = 1$
$PO \left( \frac{1}{AB} + \frac{1}{DC} \right) = 1$
... (c)
Similarly, in $\triangle ABC$, since $QO \parallel AB$, $\triangle CQO \sim \triangle CAB$.
$\frac{QO}{AB} = \frac{CQ}{CB}$
... (d)
In $\triangle BCD$, since $QO \parallel DC$, $\triangle BQO \sim \triangle BCD$.
$\frac{QO}{DC} = \frac{BQ}{BC}$
... (e)
Adding equations (d) and (e):
$\frac{QO}{AB} + \frac{QO}{DC} = \frac{CQ}{CB} + \frac{BQ}{BC}$
$QO \left( \frac{1}{AB} + \frac{1}{DC} \right) = \frac{CQ+BQ}{CB} = \frac{CB}{CB} = 1$
$QO \left( \frac{1}{AB} + \frac{1}{DC} \right) = 1$
... (f)
From equations (c) and (f), both expressions are equal to 1.
$PO \left( \frac{1}{AB} + \frac{1}{DC} \right) = QO \left( \frac{1}{AB} + \frac{1}{DC} \right)$
Dividing both sides by $\left( \frac{1}{AB} + \frac{1}{DC} \right)$, we get:
$PO = QO$
Hence, Proved.
Question 16. In Fig. 6.22, line segment DF intersect the side AC of a triangle ABC at the point E such that E is the mid-point of CA and ∠AEF = ∠AFE . Prove that $\frac{BD}{CD}$ = $\frac{BF}{CE}$ .
[Hint: Take point G on AB such that CG || DF.]
Answer:
Given:
In $\triangle ABC$, a line segment DF intersects side AC at point E.
E is the midpoint of side CA, which means $AE = EC$.
It is also given that $\angle AEF = \angle AFE$.
To Prove:
$\frac{BD}{CD} = \frac{BF}{CE}$
Construction:
Take a point G on the side AB such that the line segment CG is parallel to DF.
$CG \parallel DF$
Proof:
In $\triangle AFE$, we are given that:
$\angle AEF = \angle AFE$
(Given)
In a triangle, sides opposite to equal angles are equal. Therefore, in $\triangle AFE$:
$AE = AF$
(Sides opposite to equal angles)
We are also given that E is the midpoint of CA, so:
$AE = EC$
(Given)
From the above two equations, we can conclude:
$AF = EC$
... (i)
Now, consider the triangle $\triangle ACG$.
By construction, $CG \parallel DF$. Since E and F are points on the line DF, we have $EF \parallel CG$.
In $\triangle ACG$, the line segment EF is parallel to the side CG and intersects sides AC and AG at E and F respectively.
By the Basic Proportionality Theorem (BPT):
$\frac{AE}{EC} = \frac{AF}{FG}$
Since E is the midpoint of AC, $AE = EC$, which means $\frac{AE}{EC} = 1$.
$1 = \frac{AF}{FG}$
$AF = FG$
... (ii)
Now, consider the triangle $\triangle BDF$.
By construction, $CG \parallel DF$. The line segment CG intersects side BD at C and side BF at G.
By the Basic Proportionality Theorem (BPT) applied to $\triangle BDF$:
$\frac{BC}{CD} = \frac{BG}{GF}$
Using the property of Componendo, we add 1 to both sides:
$\frac{BC}{CD} + 1 = \frac{BG}{GF} + 1$
$\frac{BC+CD}{CD} = \frac{BG+GF}{GF}$
From the figure, we can see that $BC+CD = BD$ and $BG+GF = BF$.
$\frac{BD}{CD} = \frac{BF}{GF}$
... (iii)
From equations (i) and (ii), we have $EC = AF$ and $AF = FG$. Therefore:
$EC = FG$
Now, substitute $FG$ with $CE$ in equation (iii):
$\frac{BD}{CD} = \frac{BF}{CE}$
Hence, Proved.
Question 17. Prove that the area of the semicircle drawn on the hypotenuse of a right angled triangle is equal to the sum of the areas of the semicircles drawn on the other two sides of the triangle.
Answer:
Given:
A right-angled triangle, let's call it $\triangle ABC$, with the right angle at B.
Let the lengths of the two legs be $AB=a$ and $BC=b$, and the length of the hypotenuse be $AC=c$.
Three semicircles are drawn with diameters AB, BC, and AC respectively.
To Prove:
The area of the semicircle drawn on the hypotenuse (AC) is equal to the sum of the areas of the semicircles drawn on the other two sides (AB and BC).
Area(Semicircle on AC) = Area(Semicircle on AB) + Area(Semicircle on BC)
Proof:
Since $\triangle ABC$ is a right-angled triangle, the lengths of its sides are related by the Pythagorean theorem:
$AB^2 + BC^2 = AC^2$
$a^2 + b^2 = c^2$
... (i)
The area of a semicircle with diameter $d$ (and radius $r = d/2$) is given by the formula:
Area = $\frac{1}{2} \pi r^2 = \frac{1}{2} \pi \left(\frac{d}{2}\right)^2 = \frac{\pi d^2}{8}$
Now, let's calculate the areas of the three semicircles.
1. Area of the semicircle on side AB (diameter $a$):
$A_{AB} = \frac{\pi a^2}{8}$
2. Area of the semicircle on side BC (diameter $b$):
$A_{BC} = \frac{\pi b^2}{8}$
3. Area of the semicircle on the hypotenuse AC (diameter $c$):
$A_{AC} = \frac{\pi c^2}{8}$
We want to prove that $A_{AC} = A_{AB} + A_{BC}$.
Let's evaluate the sum of the areas of the semicircles on the two legs:
$A_{AB} + A_{BC} = \frac{\pi a^2}{8} + \frac{\pi b^2}{8}$
Factor out the common term $\frac{\pi}{8}$:
$A_{AB} + A_{BC} = \frac{\pi}{8} (a^2 + b^2)$
From the Pythagorean theorem (equation i), we know that $a^2 + b^2 = c^2$. Substitute this into the expression:
$A_{AB} + A_{BC} = \frac{\pi}{8} (c^2) = \frac{\pi c^2}{8}$
This result is exactly the expression for the area of the semicircle on the hypotenuse, $A_{AC}$.
Therefore, we have shown that:
$A_{AC} = A_{AB} + A_{BC}$
Hence Proved.
Question 18. Prove that the area of the equilateral triangle drawn on the hypotenuse of a right angled triangle is equal to the sum of the areas of the equilateral triangles drawn on the other two sides of the triangle.
Answer:
Given:
A right-angled triangle, let's call it $\triangle ABC$, with the right angle at B.
Let the lengths of the two legs be $AB=a$ and $BC=b$, and the length of the hypotenuse be $AC=c$.
Three equilateral triangles are drawn on the sides AB, BC, and AC, using these sides as their bases.
To Prove:
The area of the equilateral triangle on the hypotenuse (AC) is equal to the sum of the areas of the equilateral triangles on the other two sides (AB and BC).
Area($\triangle$ on AC) = Area($\triangle$ on AB) + Area($\triangle$ on BC)
Proof:
As $\triangle ABC$ is a right-angled triangle, its sides are related by the Pythagorean theorem:
$AB^2 + BC^2 = AC^2$
$a^2 + b^2 = c^2$
... (i)
The area of an equilateral triangle with side length $s$ is given by the formula:
Area = $\frac{\sqrt{3}}{4} s^2$
Now, let's calculate the areas of the three equilateral triangles.
1. Area of the equilateral triangle on side AB (side length $a$):
$A_{AB} = \frac{\sqrt{3}}{4} a^2$
2. Area of the equilateral triangle on side BC (side length $b$):
$A_{BC} = \frac{\sqrt{3}}{4} b^2$
3. Area of the equilateral triangle on the hypotenuse AC (side length $c$):
$A_{AC} = \frac{\sqrt{3}}{4} c^2$
We need to prove that $A_{AC} = A_{AB} + A_{BC}$.
Let's find the sum of the areas of the triangles on the two legs:
$A_{AB} + A_{BC} = \frac{\sqrt{3}}{4} a^2 + \frac{\sqrt{3}}{4} b^2$
Factor out the common term $\frac{\sqrt{3}}{4}$:
$A_{AB} + A_{BC} = \frac{\sqrt{3}}{4} (a^2 + b^2)$
From the Pythagorean theorem (equation i), we know that $a^2 + b^2 = c^2$. Substitute this into the expression:
$A_{AB} + A_{BC} = \frac{\sqrt{3}}{4} (c^2) = \frac{\sqrt{3}}{4} c^2$
This result is identical to the expression for the area of the equilateral triangle on the hypotenuse, $A_{AC}$.
Therefore, we have shown that:
$A_{AC} = A_{AB} + A_{BC}$
Hence Proved.

